こんにちは、なまはげおじさんです。
君津のさくら塾のブログへようこそ。
今日は数学のお話です。
なぜか説明できる?
昨夜の3年数学より。
問.下図の台形ABCDの面積を求めなさい。
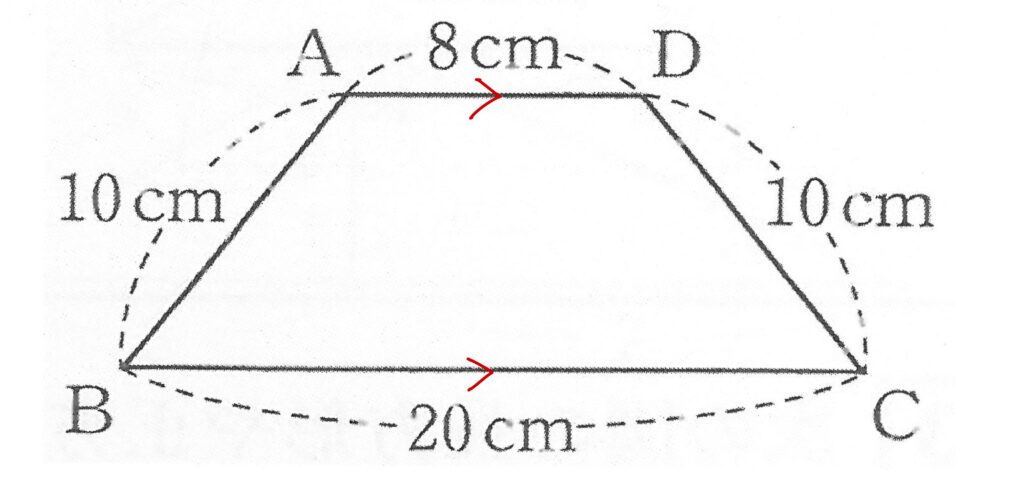
答えを求めるには
台形の面積は、
(上底+下底)×高さ×1/2
で求められます。
つまり、
(8+20)×高さ×1/2
となるので、高さが求められたら勝ちとなるわけです。
ですから、問題を次のように言い換えることもできます。
問.下図の台形ABCDの高さを求めなさい。

さて、高さを求めるにはどうすればよいでしょうか。
……補助線ですね。
「高さ」にあたる線を実際にひいてみるのです。手を動かすことが大事。そうしたら、いろいろ気づくこともあるはずです。
こんな感じ。
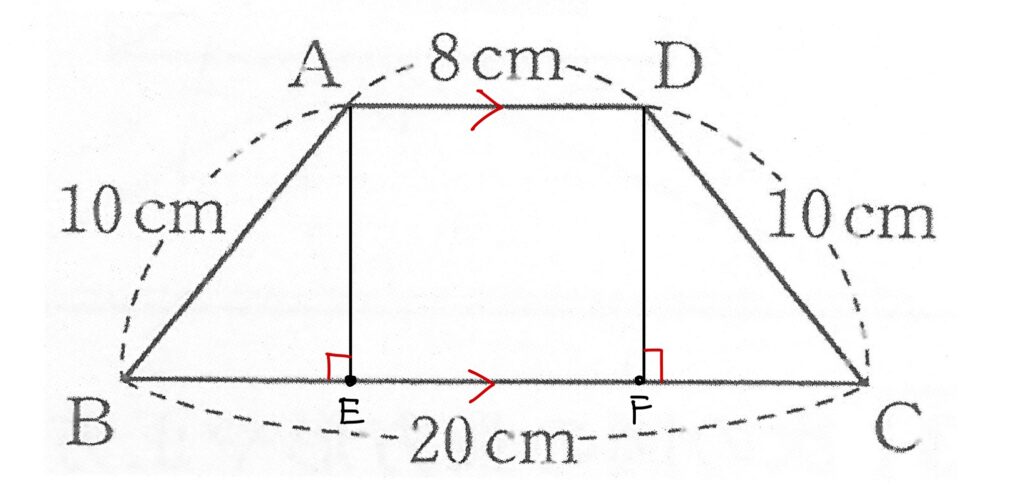
あら、わかりやすい!
2本の垂線AE,DFがひけたら、この問題はもう解けたも同然です。
図形の対称性から、
①BE=CFなので、
BE=6cm
②BE=6,AB=10なので、
△ABEは3:4:5
答.AE=8cm
となり、台形の面積は 112 であることがわかります。
解き方だけ?
実はこの問題は、教科書とテキストを使えば自学でも十分やれる基礎問題です。わざわざ進学塾の授業で扱うようなものではありません。
しかし、昨夜の授業で、私はこの問題に10分以上時間を使い、じっくり考えさせ、そして説明しました。
図形の基本的な考え方を確認することのできる、栄養たっぷりの問題だったからです。
さくら塾が教えるのは、解き方だけではありません。
ほかの問題にも通じる発想の仕方
王道の着眼点
異なるアプローチでの解き方
などなど、初見の問題への対応力を高めるために、プラスアルファをいろいろと仕込んでいます。
また、どういう力を伸ばしたいのかを常に意識して発問し(少人数なのでバンバン指名される環境)、さくらっ子の脳みそをコネコネしています。
その問題で、生徒に何を教えられるか。そこに指導者としての力量(単元観、経験、生徒ひとりひとりの学習状況の把握、……)が問われている。私はそう考えています。
昨夜の授業でも、私はさくらっ子に問いかけました。
なぜ?の追究
さくらっ子に丁寧に考えてほしかったのは、下図でなぜ BE=CF と言いきれるのか、ということ。

これ、誰でもパッと見て BE=CF だよね、と納得できちゃうんですけど、なぜそうなるのか説明しなさいと言われると、これが結構大変。
この「結構大変」なところにスポットを当てて、じっくり考えさせました。証明の基礎的な考え方や、図形の基礎的な知識を確認する絶好のチャンスだったからです。
こんな流れです。
問.BE=CFになることを証明しなさい。
①四角形AEFDは長方形である
なぜ?
→4つの内角がすべて等しいから
なぜすべて等しい?
→ AD//BCだから、
平行線の錯角は等しいので
②よって、AE=DF
なぜ?
→ 長方形の向かい合う辺は等しいから
③だから、△ABE≡△DCF
なぜ?
→ 直角三角形の斜辺と他の1辺がそれぞれ等しいから
④したがって、BE=CF
なぜ?
→ 合同な図形の対応する辺は等しいから
なぜそうなるの?
と次々繰り出されるいう私の問いかけに、さくらっ子たちは負けずに答えていました。
よく頑張っていましたよ。
図形の問題では、図を見てパッと気づいたこと、いわゆる「カン」によって短時間で問題を解けることもあります。
しかし、「なぜそうなるのか」を自ら問い続ける姿勢こそが数学という教科の本質です。そういう習慣のない人は応用問題にはまず歯が立ちませんし、高校入学後にどんづまりになりがち。

あれ、なんで?

気になるな……

調べてみよう!
なぜ?を追究していく姿勢そのものを育てていきたいです。
以上、昨夜の数学のお話でした。
それでは今日はこのあたりで失礼します。どうぞ健やかな一日をお過ごしください。



この記事についてのコメント