【非中受】問．正十二角形の面積を求めなさい

　
　
　
なまはげおじさんです、こんにちは。

君津のさくら塾のブログへようこそ。

今日は中３生向け、図形の問題を考えますよ。なお、画像を多用しておりますので、パソコンなど大きな画面のほうが見やすいかもしれません。
※中学入試の問題ではありません！
　
　
　

対称性、特別な角

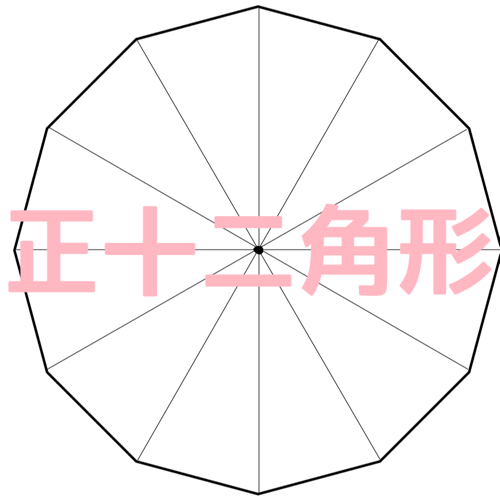
本日の問題はコチラ。
　

　
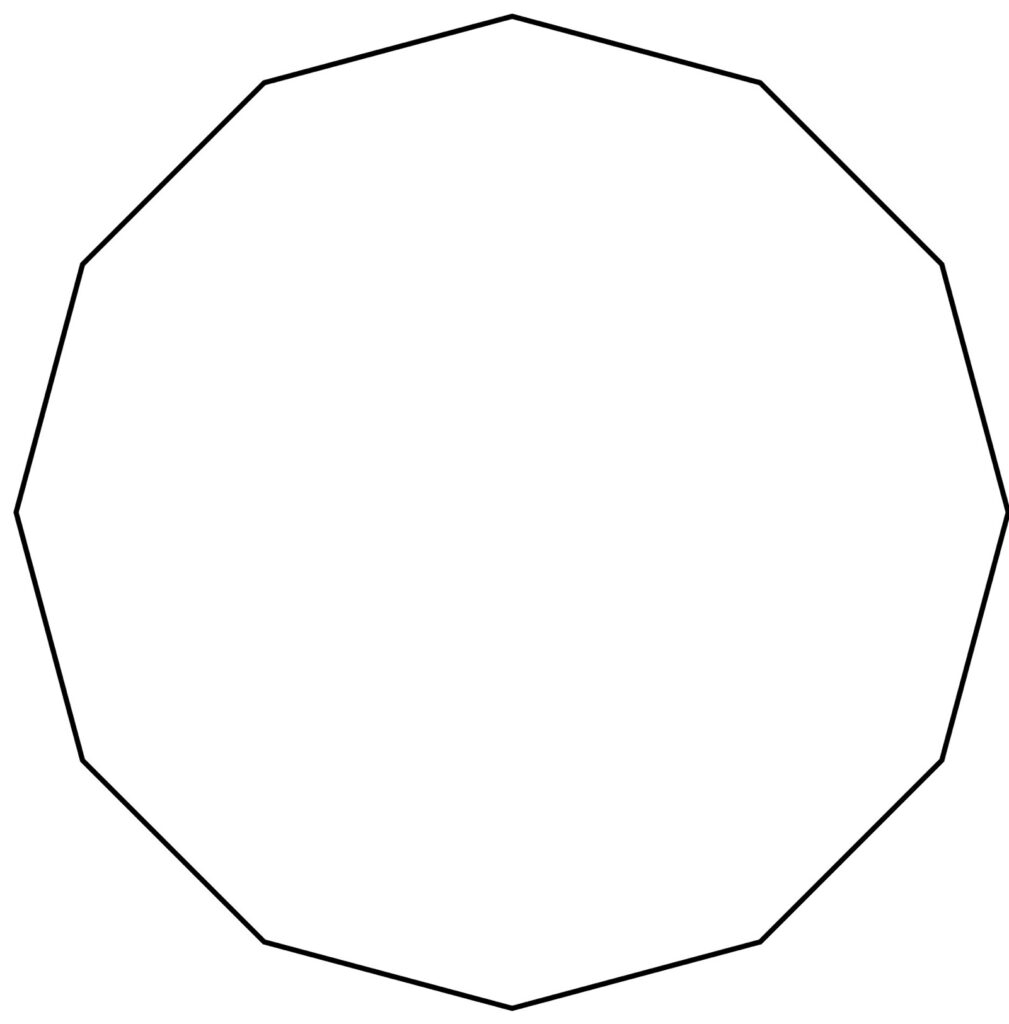
受験生のみなさんには、ノートやルーズリーフに正十二角形をササッとかいて、ぜひ挑戦していただきたい。

できるかな？？？
　
　
　
　
　

それでは、解いてみましょう。

正十二角形に対角線を引くとこうなります。
　

　
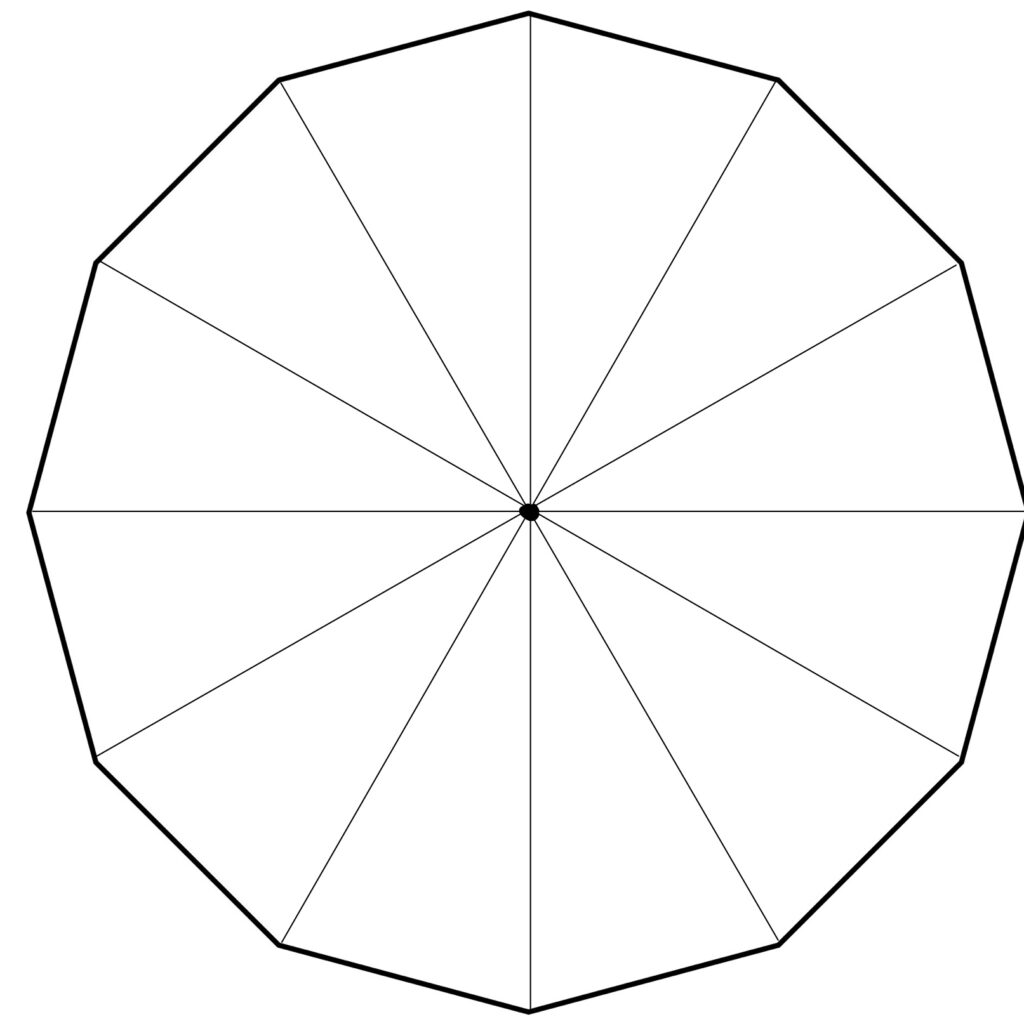
合同な三角形が、12個できるわけです。

この対称性に気づけるかどうか、これが大きなポイントですよ。
　
　

ここからは、１つの三角形のみ注目していきます。

その面積が求められたら、それを12倍すれば答えになるからです。

こういう考え方を、対称性の利用といいます。
　
　
　
360°÷12 で、30°の角を持つ三角形であることはすぐにわかりますよね。
　

　
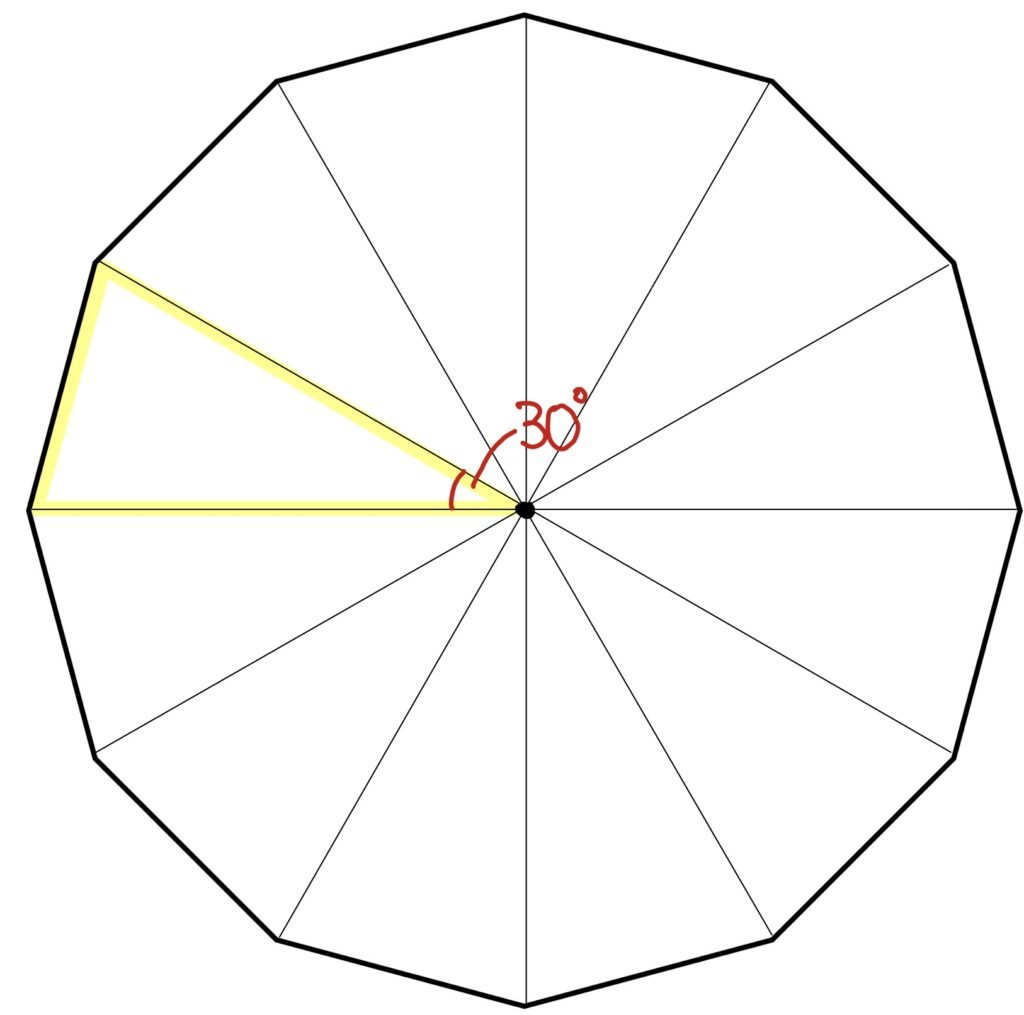
また、これが二等辺三角形であることにも、すぐに気づけるはず。

その１辺の長さを、ｘcmとします。
　
　
　

書き込んでみましょう。
　

　
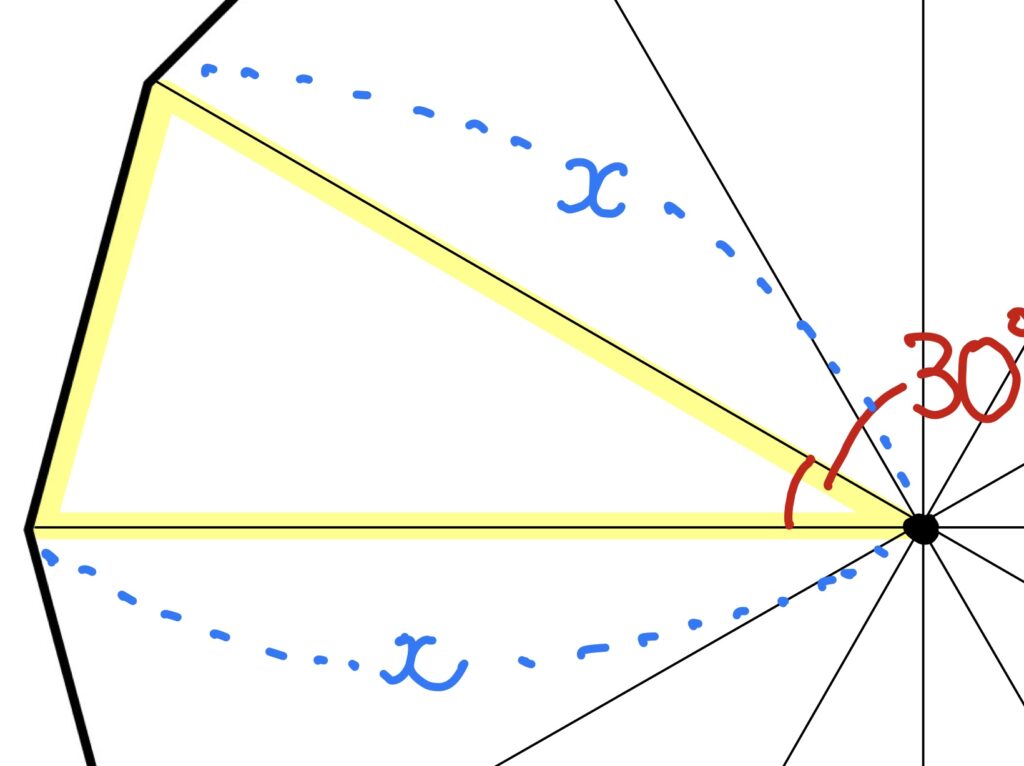
この頂角30°の二等辺三角形の面積をｘで表して、それを12倍するのです。
　

さて、どうすればいいでしょうか。
　
　
　
　
　

受験生のみなさんは、30°の三角形といえば、即座に三角定規を連想できなければなりません。

１：２：√3 のアレです。
　
　
　

そうです、補助線を加えるのです。
　

　
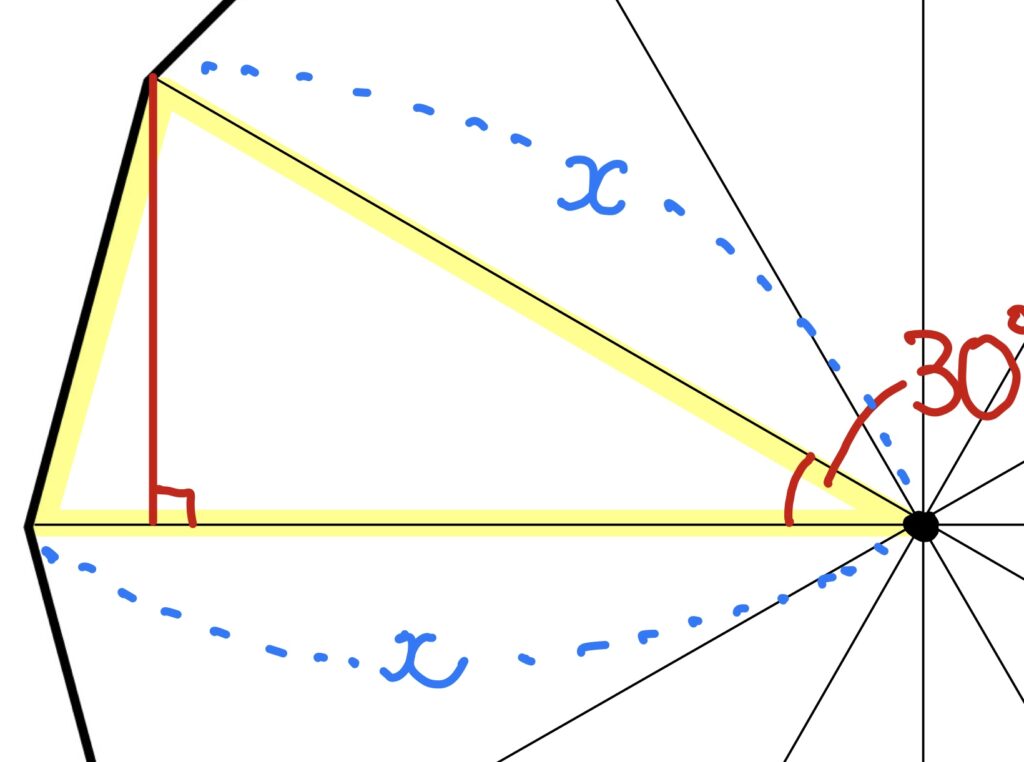
ノーヒントでこの補助線をかけた人は、自分で自分を褒めてあげてください。

素晴らしいですぞ。
　

ここからどうずればいいか、わかりますよね。
　
　
　

補助線の長さを求めるんです。

１：２：√3 を使って。
　

　
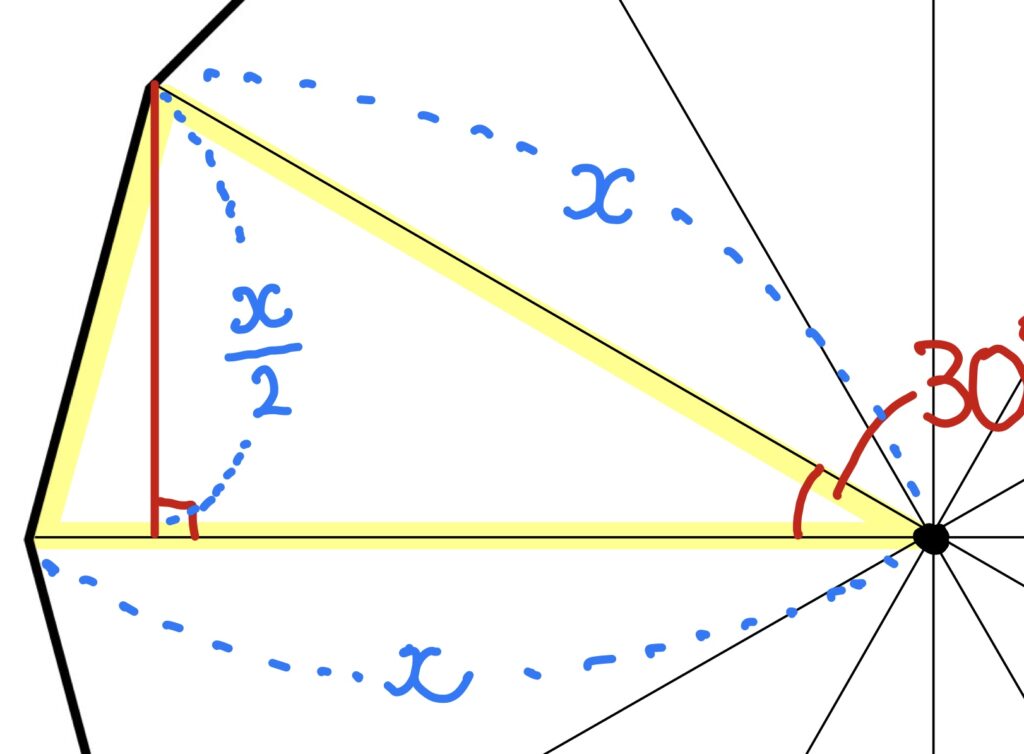
よっしゃ、これで二等辺三角形の面積を、ｘで表すことができます。

それを12倍すれば、まさに答えです！
　
　
　

こうなります。

　
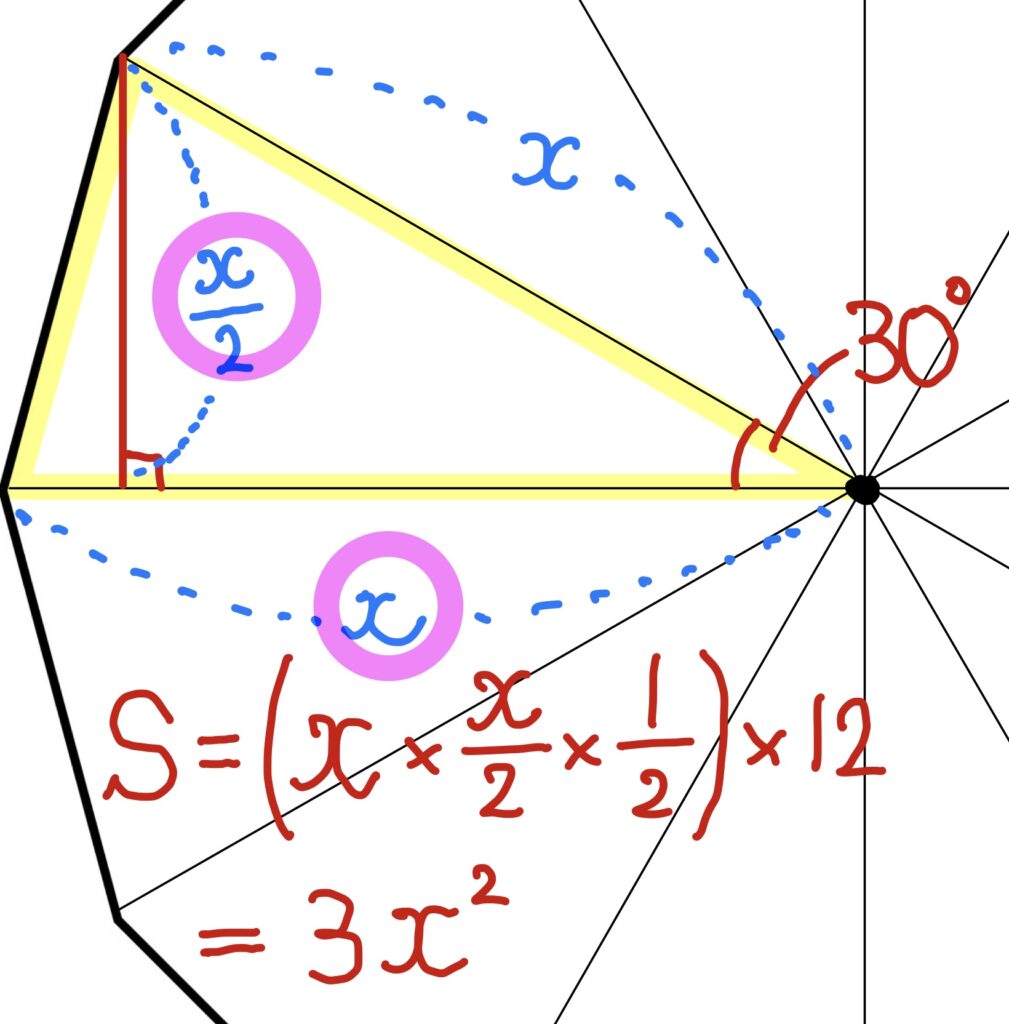
あとは、ｘの長さを求めるだけ。

左の直角三角形に三平方の定理を使ってもできますが、計算が高校生レベルになってしまいます。工夫次第でさばけないことはないのですが、かなりタイヘンです。
　

そこで今日は、さくらっ子が教えてくれたｘの長さを求める方法をご紹介します。

特別な角に注目していくのです。
　

　
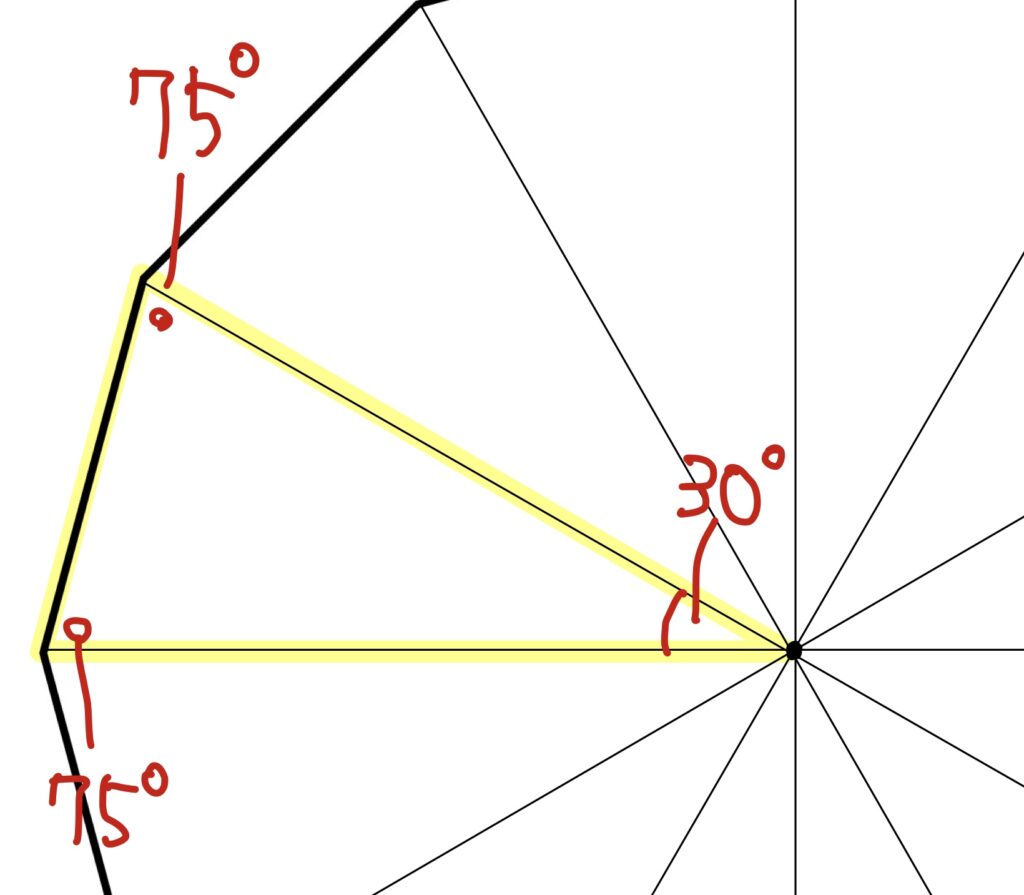
頂角30°ということは、底角は75°。

この75という数字を、特別な角に分けちゃう、という工夫をしていました。

75＝●＋▲、ということです。

わかるかな？？？
　
　
　

コチラです。
　

　
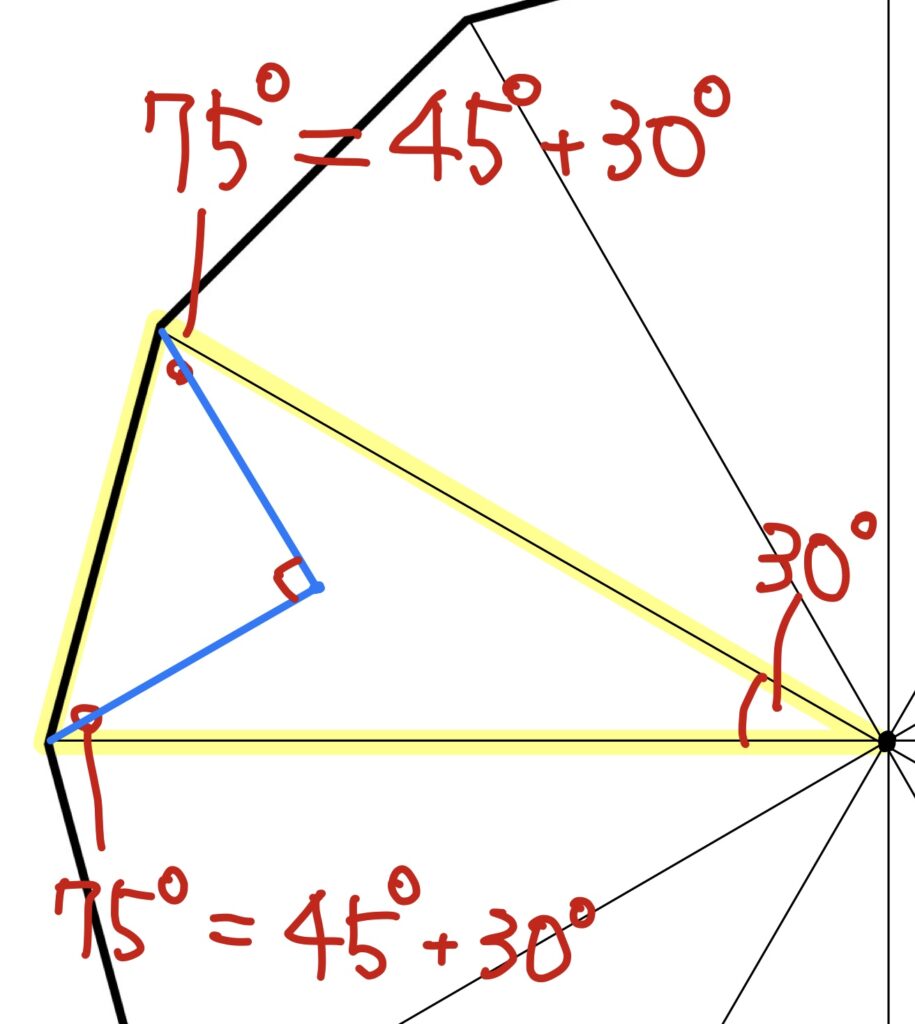
なるほど、こうすると、45°定規型が現れるんですね。
　
　

工夫はまだ続きます。

補助線を延長するのです。

コチラ。
　

　
うーむ。

１辺２cmという条件に、１：１：√2 や１：２：√3 を適用することができますぞ。

さっそくやってみましょう。
　
　
　

すると、こうなるはず。
　

　
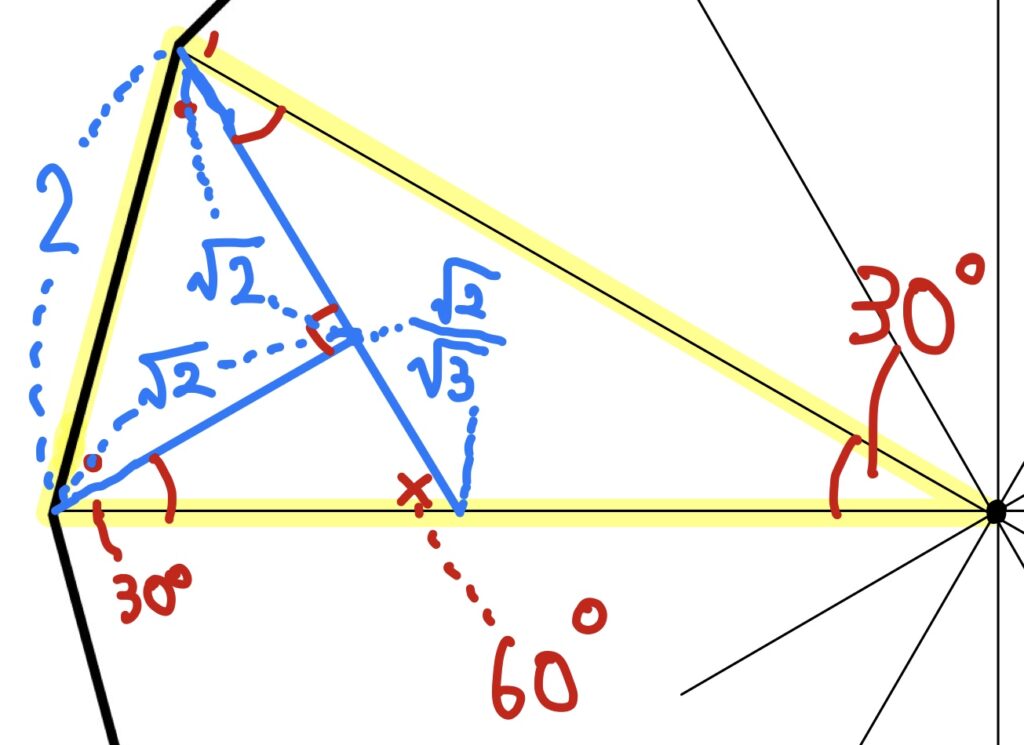
さあ、ここでさらにもうひと工夫。

上の図に、補助線を加えると、また三角定規の三角形が現れます。

どこに引くでしょうか？？？
　
　
　

ココです。
　

　
60°定規型が出てきましたよ！

１：２：√3 ですよ！
　
　
　

わかることはコチラ。
　

　
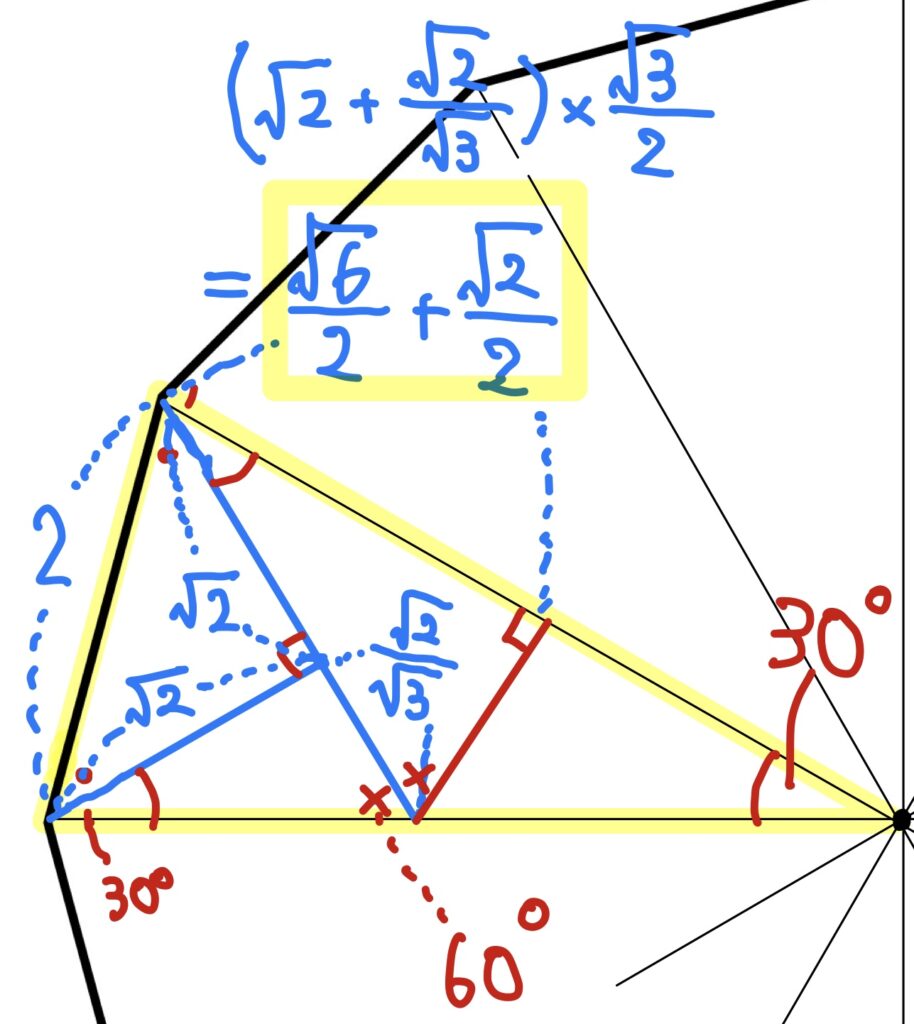
ｘの長さがわかるところまで、あと一歩。

もう気づいている人も少なくないはず。
　
　
　

コレですね。
　

　
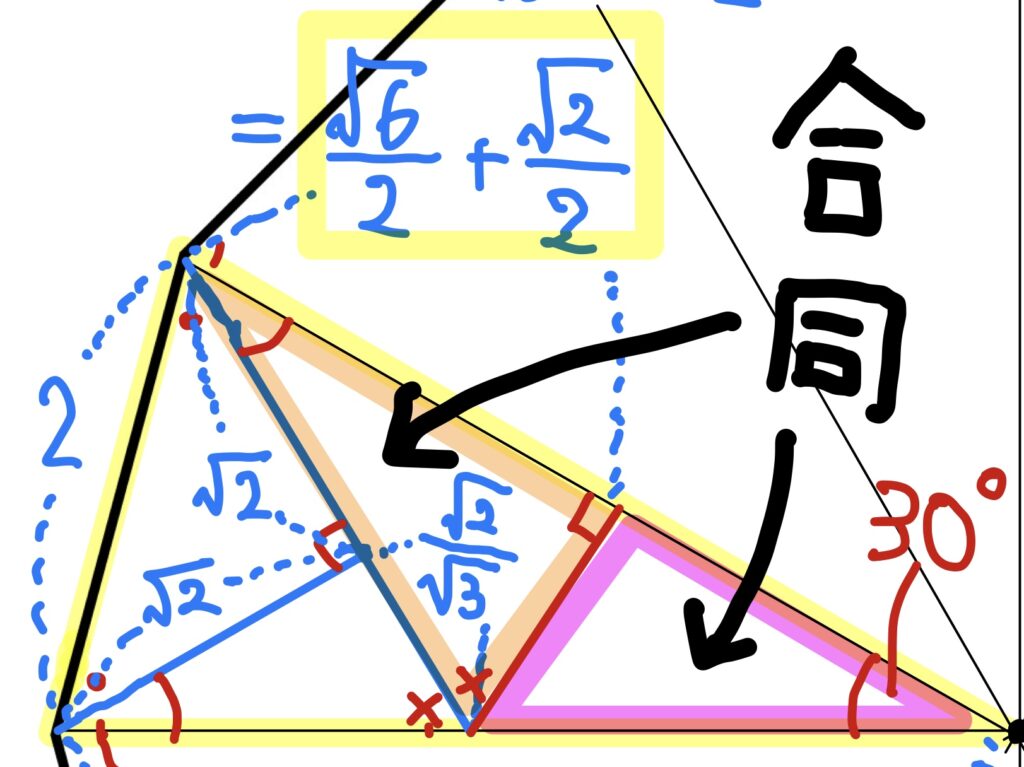
２つの直角三角形は合同なので、ｘの長さは単純に２倍すれば求められるわけです。
　
　
　

こうなります。
　

　
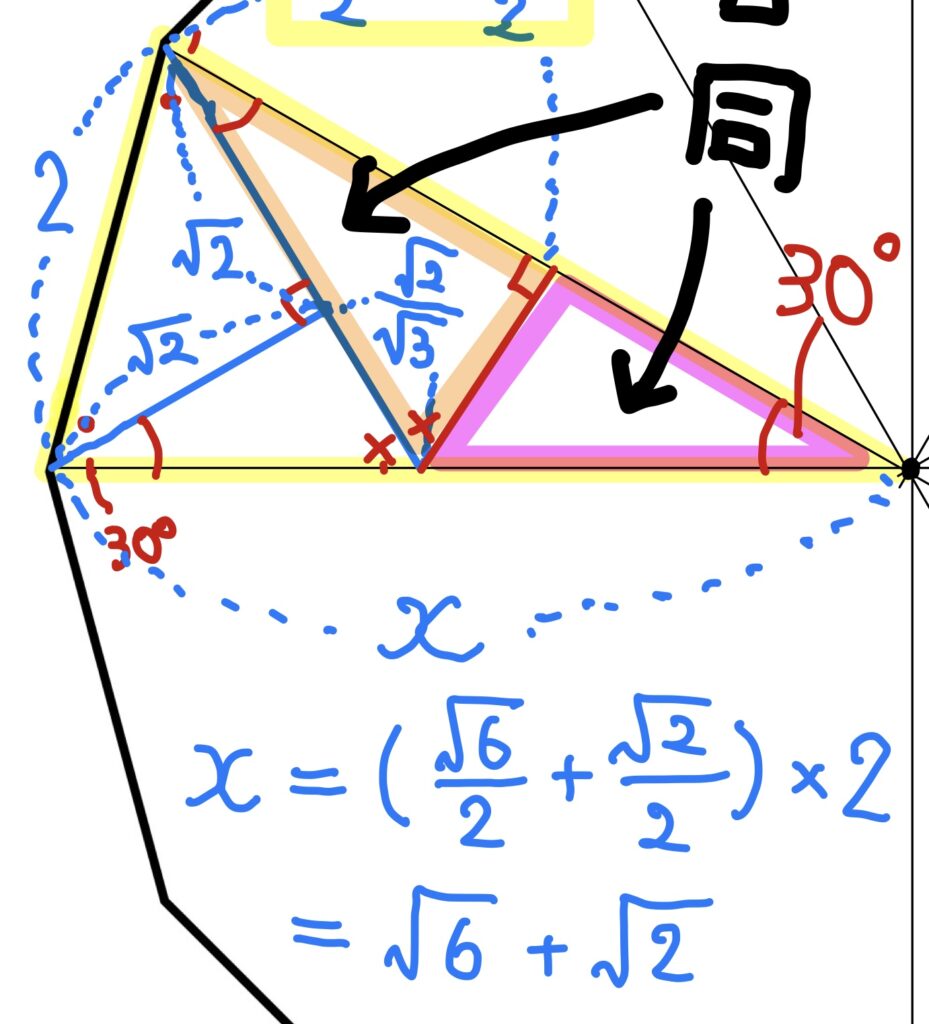
出ましたー！

　ｘ＝√6＋√2

これを代入すれば、とうとう答えがわかります！
　
　
　

はい、コチラ！
　

　
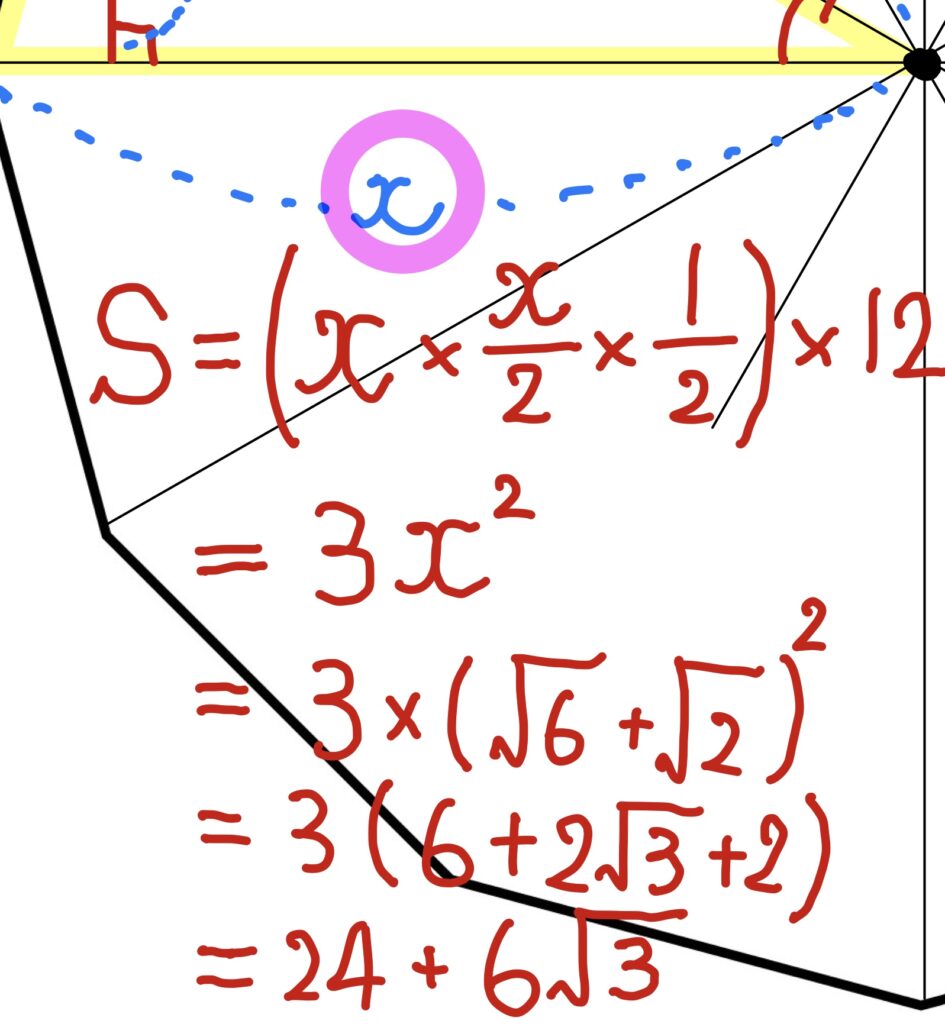
１辺２cmの正十二角形の面積は、24＋６√3 cm2 。訂正；24＋12√３㎠、計算間違えてますゴメンナサイ。
　
　
　

正十二角形の対称性を利用して、頂角30°の二等辺三角形に注目し、そして特別な角を活かすための工夫をしていく。

こう見てくると、中学数学の基本的な考え方が身についているかを問うている問題、ということがわかります。
　
　
　

図形の対称性の利用、
特別な角の利用、

これは入試本番でもあなたを助けることでしょう。
　
　
　
　
　

以上、求積問題のお話でした。

それでは今日はこのあたりで失礼します。どうぞ健やかな一日をお過ごしください。