【中学数学】関数の初心者は、これを意識するのがオススメ！

　
　
　
台風を南の空へそらす仕事で忙しいなまはげおじさんです、こんにちは。

君津のさくら塾のブログへようこそ。

今日は数学のお話。
　
　
　

関数の勉強のコツ

もう９月も半ば。

学校の数学の授業は、どの学年も関数ではないでしょうか。
　

関数の単元って、どこか抽象的なところがありません？
（あるよね）

気をつけないと、自分が何をやっているのかわからなくなっちゃいます。
　

例えば、変化の割合。

例えば、ｙの変域を求める。

例えば、中点の座標を求める。
　

そのどれもが基礎的で難しくはない。

だから正答することはできる。

でも、
　

……で、これはいったい何をしているんだろう？？？

　
と疑問を抱くことはないですか。
（あるある）

上に「抽象的」と書いたのは、そういうことですな。
　

関数の単元って、初学者にとってはハードルが高いんです。

勉強していても、
　

ヨシ、わかってきたゾ！

　
となりにくいんですよ。
　
　
　

そんなあなたに、関数の勉強のコツを教えますね。
　

自分が何をやっているのかわからなくなってきたら、図に表してみるんです。

ｘ軸とｙ軸をサッと書いて、グラフにしたり、座標を確認したり。

すると、今あなたがやっていることが、ハッキリわかるようになりますよ。
　
　
　

例えば、中点の座標の求め方。

ｘ座標同士を足して２で割る、
ｙ座標同士を足して２で割る。

うん、答えは出せる。

カンタンだし。

でも、コレっていったい何やってるんだろ？？？
　

そう感じたら、図で表してみましょう。
　

まずは座標軸をササッ。
　
　
　

　
　
　
次に、点Ａと点Ｂを書き込みます。
　
　
　

　
　
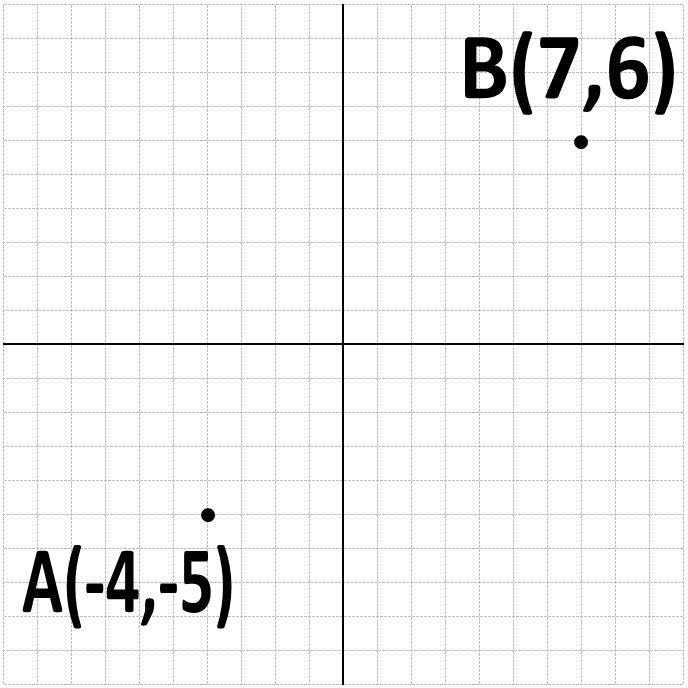
「中点」とは、真ん中の点のこと。

つまり、……
　
　
　

　
　
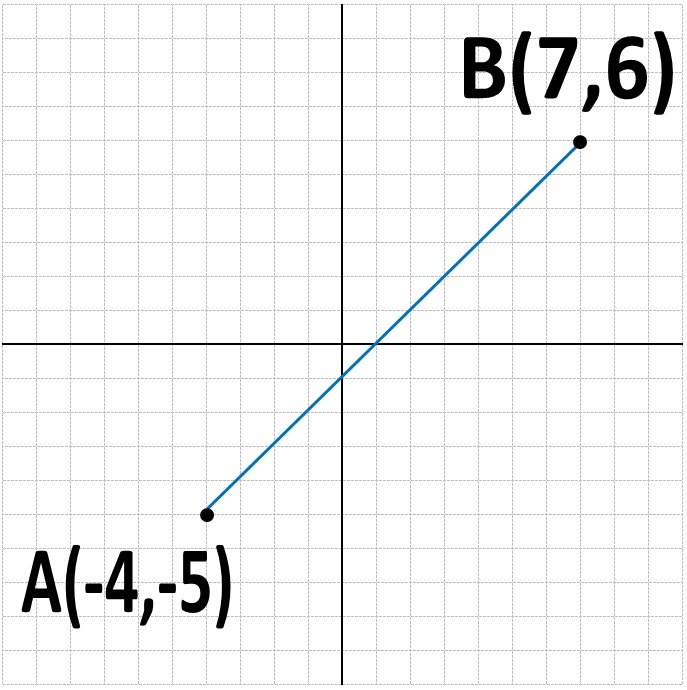
この線分ＡＢの真ん中の点の場所を求めていたんです。
　
　

　
　
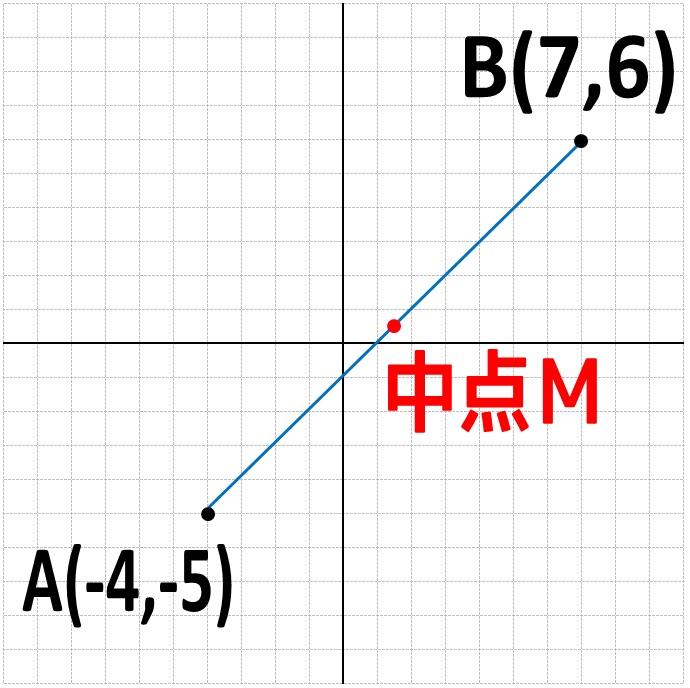
どうかな。

やっていることがハッキリ見えてきたでしょう？
　

あー、だからｘ座標同士を足して２で割ってたのか！

　
図で表して考える、

これが関数の勉強のコツなんです。
　
　

関数は、図に表して考えるべし

　
図に表すと、関数と図形をMIXさせて考えることもできるようになりますぞ。
図形の問題を、関数のワザでズバッと解くこともできるようになるのです。

実際に図を書かなくても、頭の中にイメージするだけでもＯＫ。

関数は図に表して考える、

これを意識してみてください。
　
　
　
　
　

以上、数学のお話でした。

それでは今日はこのあたりで失礼します。どうぞ健やかな一日をお過ごしください。