こんにちは、なまはげおじさんです。
君津のさくら塾のブログへようこそ。
今日は中3生向けのお話、リライトです。
ちょっと濃いめの数学のお話
まず、「線分の比と平行線」の学習を終えた人向けに出題します。数学大好きなあなた、ぜひ挑戦してみてください。

自分なりの答えが出た人は、スクロールしてみてください。
答えは、39:28 です。
合ってましたか?
「平行線を利用して相似な三角形を見つける」ことを意識すると、
補助線をひけばいいのでは?
という発想にたどり着くはず。
例えばこう。
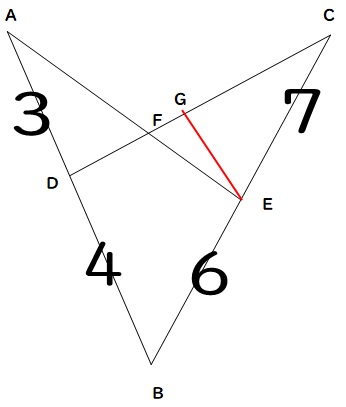
AB // GE となるように点GをCD上にとるんです。
すると、相似な三角形のペアが、2組見つかるはず。
こちら解答例です。


補助線をどこにひくのか、
それが難しいんですよね、コレ。
実は、まったく補助線をひかない解き方もあります。
解答例、その2。

この途中式は『ひと筆書きの定理』によるもの。
高校数学で学ぶ「メネラウスの定理」のことですが、さくら塾では覚えやすいのでこう呼んでいます。
『ひと筆書きの定理』とは?
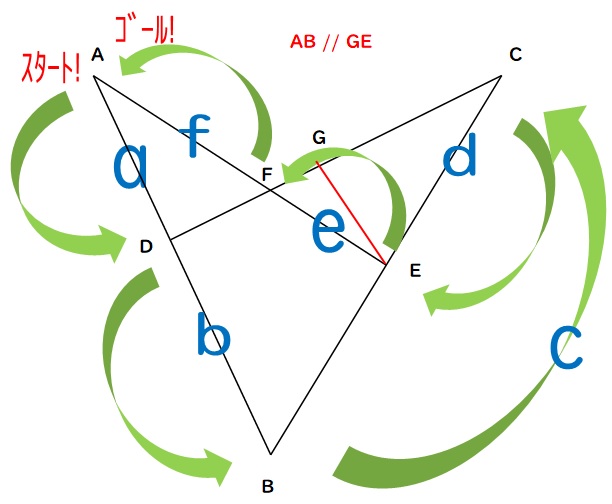
『ひと筆書きの定理』とは、下図のようなキツネ型の図に対して使えるものです。
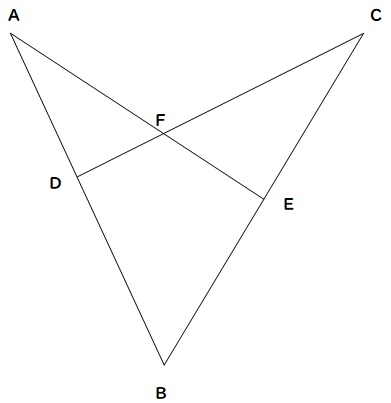
キツネ型の「耳」にあたる頂点がスタート、と覚えてください。
この図では、頂点Aか頂点Cから始めるわけです。
こんな感じ。
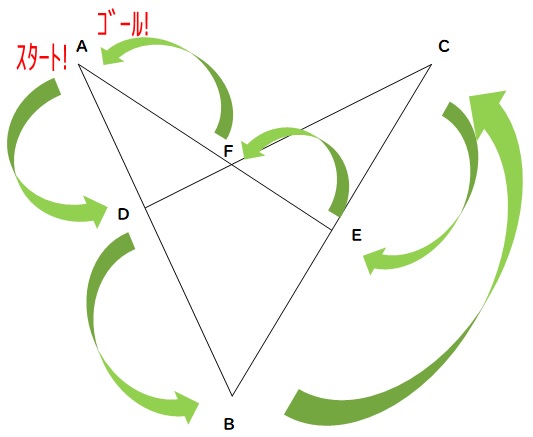
このとき、次のような関係式が成り立ちます。
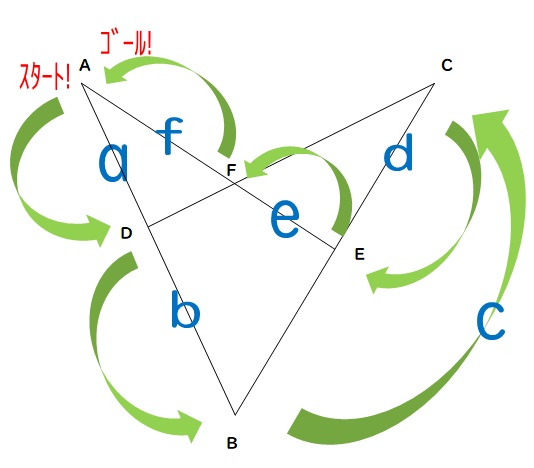
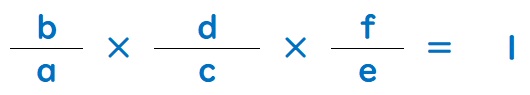
最初の問題に戻って再挑戦してみてください。どうですか、ビックリするくらいカンタンに解けちゃうでしょ?
『ひと筆書きの定理』の証明
なぜ『一筆書きの定理』が成り立つのか?
そんな疑問を抱いてしまったあなた、数学のセンスがキラキラしてますよ!
……実はこれ、中学数学の知識でも十分証明できちゃうんです。
情熱あふれるあなたへ、
証明の方針と、
最初のカギについて、
それぞれアドバイスしますね。
証明の方針
まず、方針について。
平行線を利用して相似な三角形を見つける。

「平行線を利用して相似な三角形を見つける」というのが、この単元の裏テーマ。
でも、この図のままでは、平行線も、相似な三角形もありませんね。
ということは……?
……そう、補助線を引くんです!
それも、何かと平行な補助線を。
どこに補助線を引くべきか
証明するための最初のカギは、
どこに
どのような
補助線を引くかです。
いろいろな方法があります。
一例を紹介しますね。
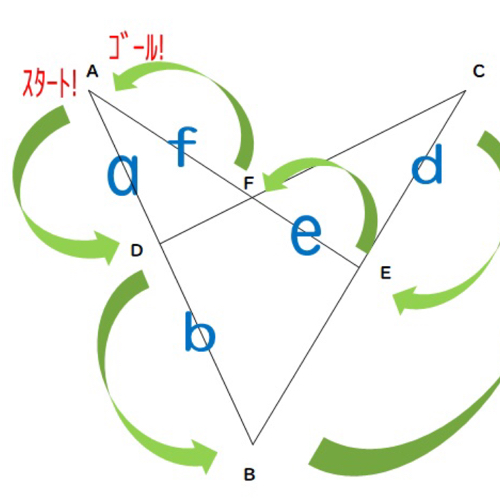
こんな補助線を引いてみてください。
さっきと同じです笑
上図を見て、相似な三角形のペアが見つかりますか?
2ペアありますよね。
見つかりましたか?
△CGE∽△CDB、
△ADF∽△EGF、
この2ペアです。
これらを使って比例式をつくり、整理して、下の式に代入。
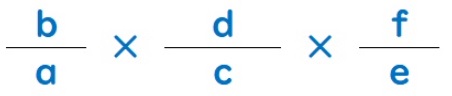
すると、うまいこと文字がバンバン約分されて笑、気がつけば 1 になります。
証明終了。
ただし、途中の計算式はちょっと大変、気合い入れて頑張ってください。
以上、濃いめの数学のお話でした。
それでは今日はこのあたりで失礼します。どうぞ健やかな一日をお過ごしください。



この記事についてのコメント