なまはげおじさんです、こんにちは。
君津のさくら塾のブログへようこそ。
今日は偏差値のお話、リライトです。
中学生でもわかる偏差値のお話 1
あまり突っ込みすぎると高校数学の解説になってしまいますので、そういったところはばっさりカットしていきますね。
偏差値はこう求めます
偏差値を求めるには、公式があります。
高校の数学です。
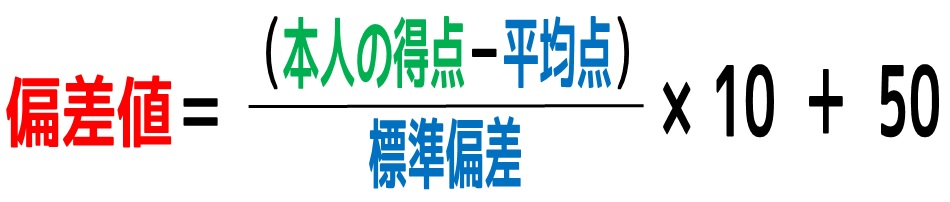
偏差値のイメージをつかむために、例を3つ挙げてみます。
例1;「本人の得点」が「平均点」とぴったり同じ
分数のところが 0 になるので、
偏差値= 0 × 10 + 50
= 0 + 50
= 50
となり、偏差値は 50 となります。
例2;「本人の得点」が「平均点」より高い
分数のところが例えば 1 になったら、
偏差値= 1 × 10 + 50
= 10 + 50
= 60
となり、偏差値は 60 になります。
例3;「本人の得点」が「平均点」より低い
分数のところが例えば -0.5 になったら、
偏差値= -0.5 × 10 + 50
= -5 + 50
= 45
ですから、偏差値は 45 ですね。
まとめるとこうなります。
得点が平均点より高い
→ 偏差値>50
得点が平均点と等しい
→ 偏差値=50
得点が平均点より低い
→ 偏差値<50
シンプルですね。
それは、「平均点」と「標準偏差」という用語について簡潔に説明します。
「平均点」とは
そのテストを受験した人全員の平均点。
計算は簡単で、全員の得点を足して、それを人数で割れば求められます。
「標準偏差」とは
受験生全員の得点のばらつきを示す値です。
その求め方はかなりややこしいので割愛し、用語の意味だけお伝えします。
例えば、「標準偏差」が 15.0 だとしたら、平均点± 15.0 の範囲の中にほとんどの受験生がいる、と推定することができるのです。
定期テストなどは、できれば「標準偏差」は小さい値になるべきです。
学年であまりに得点のばらつきが激しいと、どのレベルに照準を合わせた授業をすればいいのか判斷しづらくなり、授業を進めるのが難しくなってしまいますから。
「本人の得点」だけでは決まらない
この公式からわかるのは、偏差値を決定する要素は「本人の得点」だけではないということ。
受験生全員の
「平均点」
「標準偏差」
に大きく左右されるのです。
ちょっと例を作ってみました。
マヤくんは、2回のテストの両方で100点満点、平均点はどちらも50点でした。
さて偏差値はどうなったかな・・・。
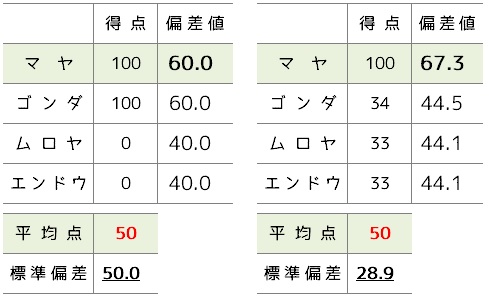
60.0 と 67.3 、驚くほど差が開いてしまいました。
不思議ですね。
「標準偏差」の値にご注目。
ここが大きいと、偏差値は伸びにくくなるんです。
「標準偏差」がごく小さい例と、ものすごく大きい例を並べてみます。
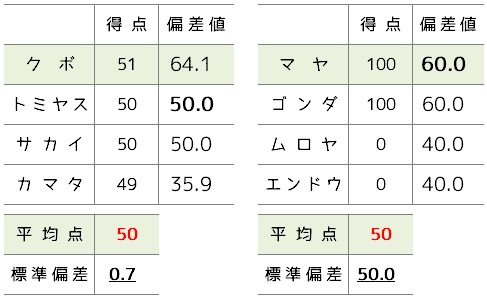
どちらのテストも平均点は50点。
しかし、100点をとったマヤくんよりも、51点のクボくんの方が偏差値がずっと高くなってしまいました。
よく見ると、カマタくんなんて平均点より1点低かっただけなのに、偏差値35.9ですよ。
これはショックだろうなぁ。
標準偏差の値が小さすぎるとこうなっちゃうんですね。
標準偏差が大きな値
→ ばらつきが大きい
→ 高い偏差値は出にくい
標準偏差が小さな値
→ ばらつきは小さい
→ 高い偏差値が出やすい
いくつか例を挙げて偏差値について見てきました。
「本人の得点」がどれだけ良くても、それだけで高い偏差値が出るわけではないということが伝わったらうれしいです。
……続きは後編で。
それでは今日はこのあたりで失礼します。どうぞ健やかな一日をお過ごしください。




この記事についてのコメント