なまはげおじさんです、こんにちは。
君津のさくら塾のブログへようこそ。
中3生向けの数学のお話、リライト。
相似な三角形を探すのです
中3生のみなさん、数学の問題を出しますよ。「相似」の学習を終えているあなた、ぜひ挑戦してください。
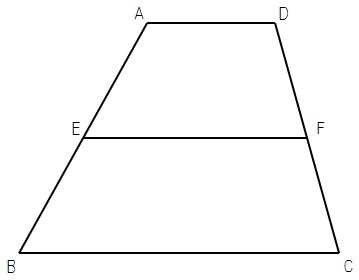
さまざまなテキストや問題集に掲載されている基礎問題です。受験生のみなさん、ノーヒントで解けたでしょうか。
……じゃぁ答えを発表しますよ。
答.EF=11
解説です。
問題文の「点E,Fはそれぞれ辺AB,DCの中点であり」から、

中点連結定理かな?
と発想できたらOKですね。
ただし、中点連結定理は三角形に対して使えるものなので、このままでは手が出せません。
そこで、補助線の出番です。
補助線を書き込むことで、相似な三角形を探してみるのです。
例えばこんな感じ。
対角線ACをひきます。
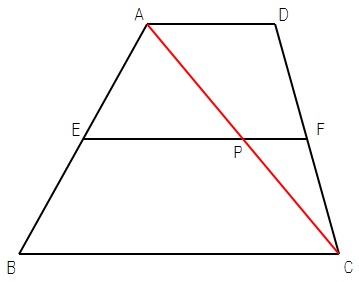
上図で、点PはACの中点です。
質問1;これを証明しなさい。
よって、△ABCにおいて、中点連結定理より、
EP=7
△CADについても同様に、
FP=4
したがって、
EF=EP+FP=11
【質問1の解答】
仮定より、 EP//BC だから、平行線の同位角は等しいので、
∠AEP=∠ABC
∠APE=∠ACB
2組の角がそれぞれ等しいので、
△AEP∽△ABC
相似な図形は対応する辺の比が等しいので、
AP:AC=AE:AB=1:2
よって、AP=PCだから、点PはACの中点である。
この中点連結定理、シンプルな上にわかりやすいので受験生に大人気です。問題文に「中点」とあるだけで、

勝った!

もらった!

5点ゲットだ!
とニヤニヤしちゃう人がいるくらい。
そんなあなたに挑戦状。
さて、できるかな???

台形の中点を結ぶと必ず上底・下底と平行になることを証明しろ、という問題です。

証明なの?

長さの話じゃないの?

ひどい、だまされた!
……などとふくれたりしないで、中3生のみなさんにはがんばって考えてみていただきたいところ。
解説は、次の4ステップでいきます。
・ヒント①
・ヒント②
・証明のおおまかな流れ
・証明(=解答例)
じゃぁもう一度図を。

下にスクロールすると、ヒント①がありますよ。
ヒント① どこかに何本か補助線をひきます

スマホの画面ではなく、ノートやルーズリーフでやってみると「あッ」とひらめきがおとずれるかもしれませんぞ。
ひらめきがおとずれなかった人、下にスクロールすると、ヒント②がありますよ。
ヒント② こんな補助線をひいてみて

上の図を見て、一気に視界が開けた人、多いんじゃないでしょうか。さっそく証明を書いてみてください。対応する頂点の順に気を配ってね。
「いやいや、いまだにわからないッス」というあなた、もうちょっと図を見て考えてみて。
EF//BCになることを証明するんだよ。
つまり、EF//BGであればいい、ということだからね。
「アカーン」というあなた、下にスクロールすると3つめのヒント、「証明の大まかな流れ」がありますよ。
証明のおおまかな流れ
・△FADと△FGCが合同だ!
・だから、点FはAGの中点だ!
・よって、△ABGで中点連結定理が使える!
・EF//BGといえる!
それでは、証明してみましょう。
証明)
上図のように補助線をひく。
△FADと△FGCにおいて、
仮定より、
FD=FC……①
AD//CGだから、平行線の錯角は等しいので、
∠FDA=∠FCG……②
対頂角は等しいので、
∠AFD=∠GFC……③
①②③より、1組の辺とその両端の角が、それぞれ等しいので、
△FAD≡△FGC
合同な図形は対応する辺が等しいから、
FA=FG
点E,FはそれぞれAB,AGの中点なので、△ABGにおいて中点連結定理より、
EF//BG
よって、
EF//BC
……となります。
ふりかえってみると、一番の難所は、やはり補助線をひくところですよね。2本。
それさえできてしまえば、あとは教科書レベルの素直な証明。

さて、この補助線の引き方、どういう発想から出てきたと思います?

与えられている仮定は「中点」だから、きっと中点連結定理を利用するんだろうなぁ

中点連結定理って、相似な三角形のお話だよね

じゃあEFを辺に持っている三角形と、それと相似な三角形をつくればいいのでは?
……とイメージできるようになれば、補助線をひけるようになると思います。
ファイト!
以上、中3生向けのお話でした。
それでは今日はこのあたりで失礼します。どうぞ健やかな一日をお過ごしください。



この記事についてのコメント