対新型コロナウイルス用ATフィールドを展開中のなまはげおじさんです、こんにちは。エヴァンゲリオンはちゃんと観たことがありませんごめんなさい。こちらは千葉県君津市、さくら塾のブログへようこそ。
今日は数学のお話です。
図をかいてみよう
3年数学「式の計算」、単元末に文字式を利用して証明する問題があります。例えばこういうものですな。
= a2 -( a + b )( a – b )
= a2 -( a2 -b2 )
= b2
「この証明自体はわかるんだけど、長方形Bの方が面積が狭くなってしまうことがどうにもピンとこないんだよねー」「なんだか不思議な気がする」というつぶやきがありましたので、ブログでとりあげてみます。
図をかくとつかみやすくなる
たいていの問題は、頭の中だけで考えるよりも、図をかいてしまった方がわかりやすくなるものです。さっそくやってみましょう。
まずは1辺a㎝の正方形A。
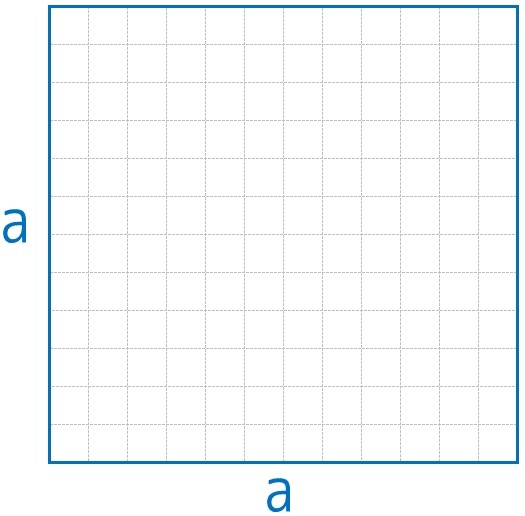
この縦をb㎝伸ばして、横をb㎝縮めた長方形。
わざと重ねてかいてみます。
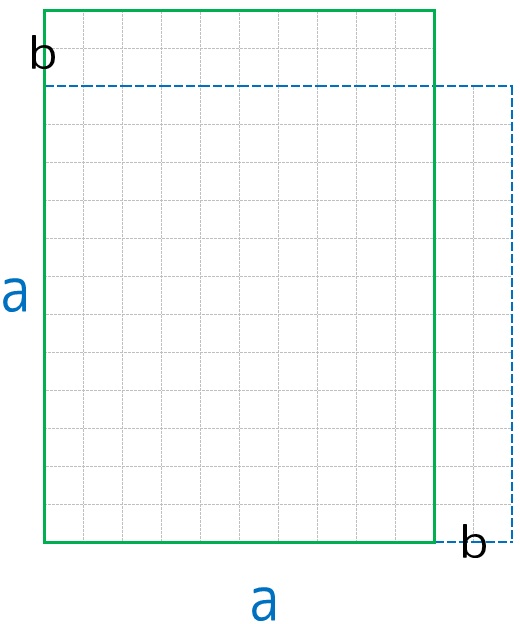
それぞれの縦・横の長さを書き込んでみましょう。
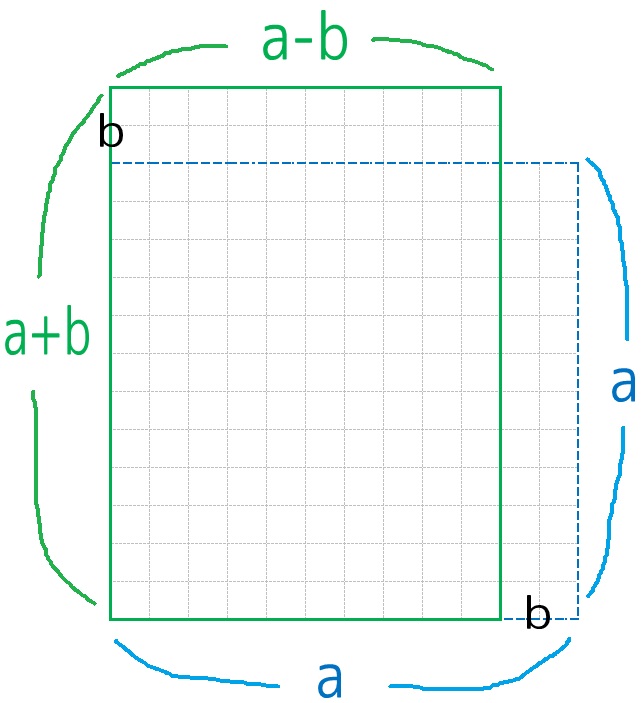
もとの正方形Aから見て、「面積が増えた部分」と、削られてしまって「面積が減った部分」があります。また、長方形Bとの「共通部分」もありますね。こんな感じ。

「増えた部分」と「減った部分」に注目して、それぞれ長さを書き込みます。

黄色い「増えた部分」と、オレンジの「減った部分」を比べるわけです。マス目を数えて計算してもいいのですが、それだとあまりに小学生っぽいので、下のように一工夫しましょうか。
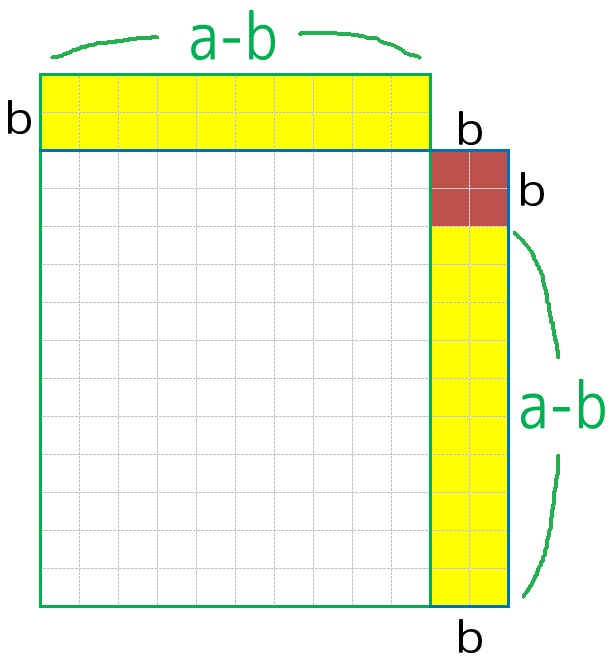
いかがでしょうか。オレンジの「減った部分」を分解してみました。
一目瞭然ですな。
長方形Bは b2 だけ面積が狭くなるわけです。
計算にしろ関数にしろ図形にしろ、頭の中だけで考えようとこだわるのはあまりよくないですよ。わかっていることを図に表すと、何かしら発見があるかもしれません。その発見したことをさらに書き込むことで、あらたなひらめきが訪れるでしょう。
図にあらわすこと、オススメですぞ。
以上、数学のお話でした。
それでは今日はこのあたりで失礼します。どうぞ健やかな一日をお過ごしください。




この記事についてのコメント