【25/05/21】明日はお休みですよ（算数クイズの解答編あり）

　
　
　
こんにちは、なまはげおじさんです。
君津のさくら塾のブログへようこそ。
　
　
　

明日22日(木)は、すでにお知らせしてあるとおり、さくら塾はお休みです。

体育祭対応です。
　

自習室も使えません。

ブルテをためにため込んでいる３年さくらっ子、間違えて明日来ないようにね。
　
　
　

これだけでブログをおしまいにしちゃうとあまりに寂しいので、先日出題していた小学生の算数の問題、解答編を掲載しますね。

まずは、お題をもう一度。
　
　

問．斜線部の図形の面積を求めなさい。
　

　
　
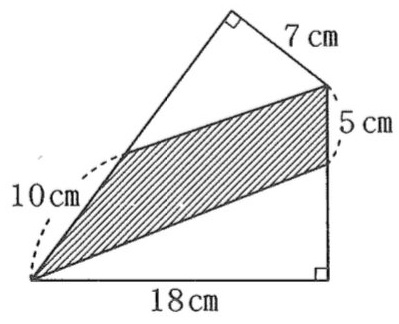
それでは解答編です。
　
　

斜線部の図形は四角形ですが、台形でも長方形でもないため、直接面積を求めることができません。

そこで、分割することにします。
　
　

　
　
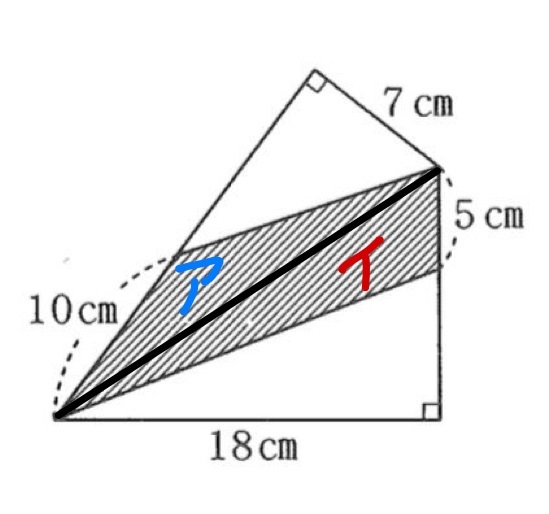
まずアの三角形の面積を求めて、

次にイの三角形の面積を求めて、

最後にそれらを足しましょう。
　
　

それでは、まずアの三角形から。
　
　

　
　
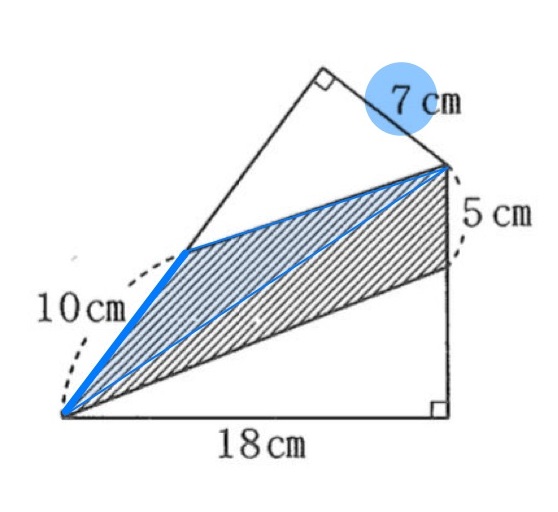
底辺10cmなので、次は高さがわかればOK。

底辺と垂直なものを探すんでしたね。

高さは７cmなので、

　10×７÷２＝35
　
　

次は、イの三角形。
　
　

　
　
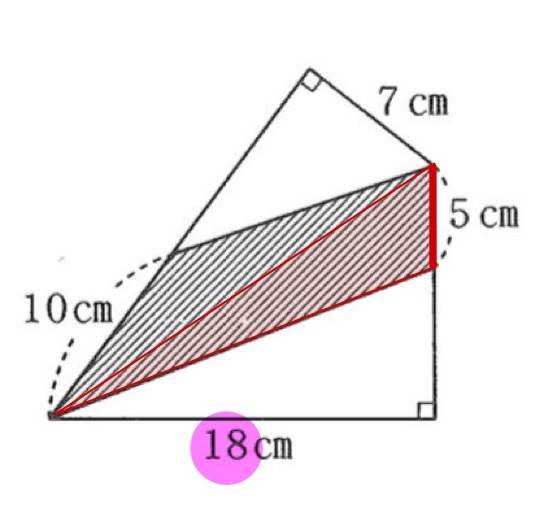
同じように考えて、

　５×18÷２＝45

２つの三角形を足せばよいので、

　35＋45＝80 cm2
　
　

「底辺と高さは垂直」であることがちゃんと身についているかのチェックができる、よい問題だと思います。
　
　
　
　
　

それでは今日はこのあたりで失礼します。どうぞ健やかな一日をお過ごしください。