なまはげおじさんです、こんにちは。
君津のさくら塾のブログへようこそ。
今日は方程式のお話です。
整数にするとラクになる
方程式も連立方程式も二次方程式も、ラストに必ずこのパターンになりますね。
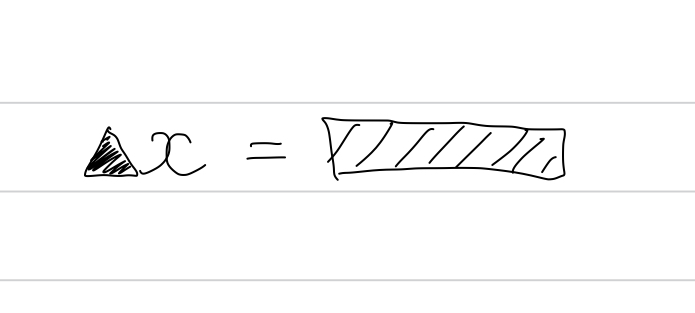
このあとに何をする……?

両辺を▲で割る
そのとおり。
例えば、1年生の基礎問題。
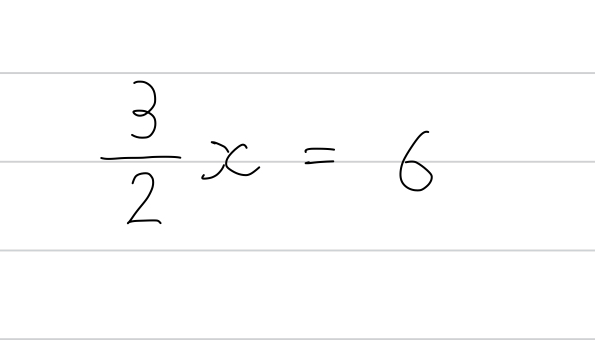
おそらく多くの人が、次のような解き方をするでしょう。
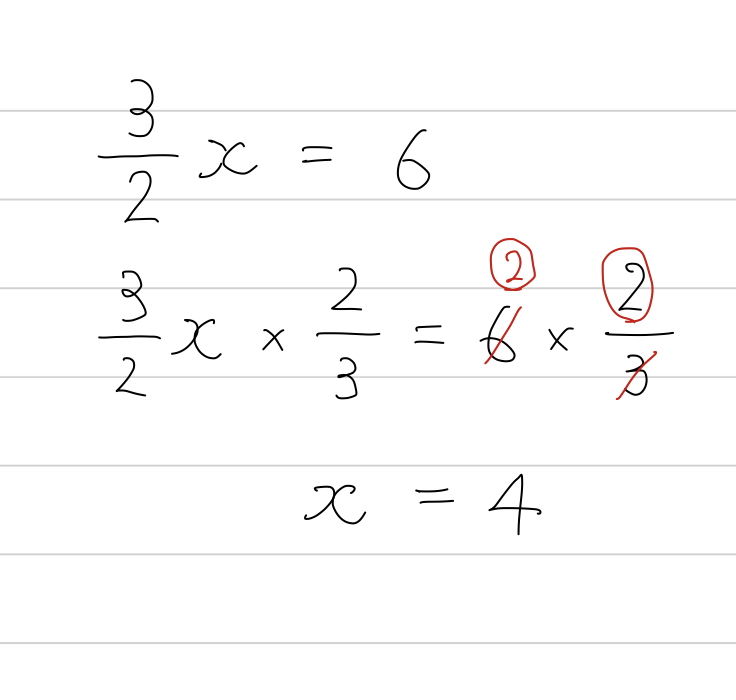
うむ、OKです。
問題ナシ。
でもね、分数がからんでくるので、逆数を書き間違えたり、約分で失敗したりと、案外ミスが出やすいんですよ、コレ。
そこで、ちょっと、ひと工夫。
こんな解き方もあります。

いかがでしょう。
カンタンに見えませんか。
並べてみましょう。

右の解き方のほうが、
計算量が少なく
速い
ことに気づけますか。
脳みそに負荷がかからないので、ミスが出にくくなるんです。
ここでの「工夫」とは……

「▲x=……」の形は、▲を整数にするとラク。
コレ、結構使えますよ。
次の例題は、2・3年生向け。
中3の冬、受験勉強で図形問題とたたかっていると、しばしばこんな計算をすることになります。
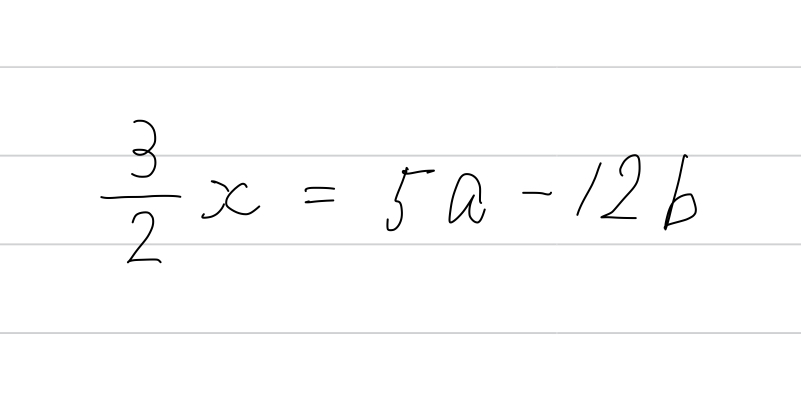
受験の図形問題は、こういうちょっと面倒な計算の連続になります。
短時間で
確実に
さばけるようにならないと。
さあ、解いてみましょう。
ほとんどの人はこうかな。

うむ、これはしんどい。ちょいと複雑なので時間もかかりそうですし、いかにもミスが出そう。
では、工夫をした解き方。
両辺に2をかけてみましょう。
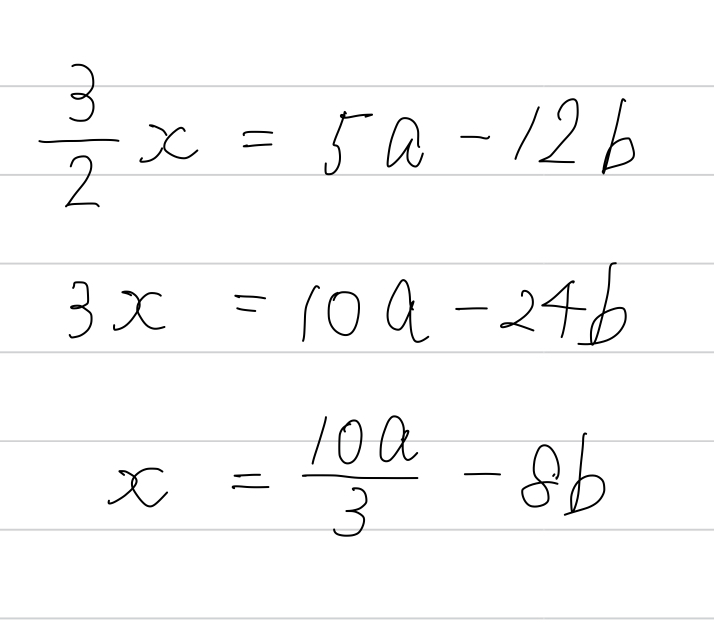
これはラクちん。
途中式もスッキリしてます。
2つの解き方を並べました。
見比べてみてください。
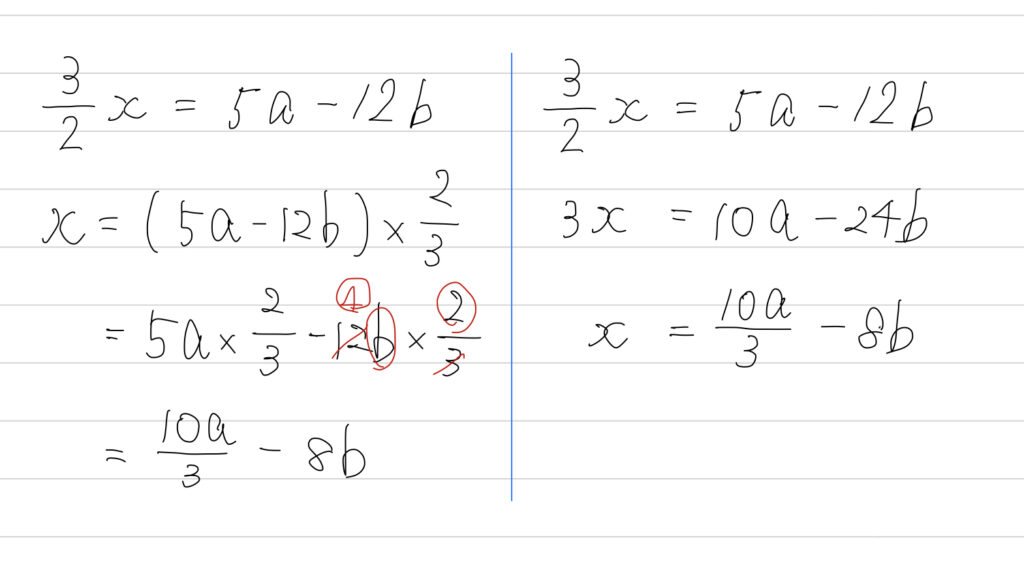
左右どっちが見やすい?
カンタンそうに見えるのはどっち?
右ですよね。
右の解き方の良さとして、途中式を書くためのスペースが狭くてもなんとかなる、という点もあります。定期テストで、計算スペースがほとんどなくて困ったことのある人もいるのでは?
方程式のラストでの計算ミスを減らすための工夫。

「▲x=……」の形は、▲を整数にするとラク。
この工夫は、3年数学でも使えます。
例えばこんな問題。
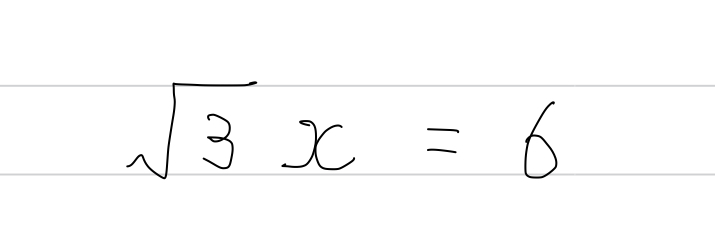
相似や三平方の定理の問題を解いていると、しょっちゅうこんな方程式を解くことになります。受験が近づいてきたこの時期であれば、3年生のみなさんには暗算でさばいてほしいところ。
多くの人がこうやるでしょう。
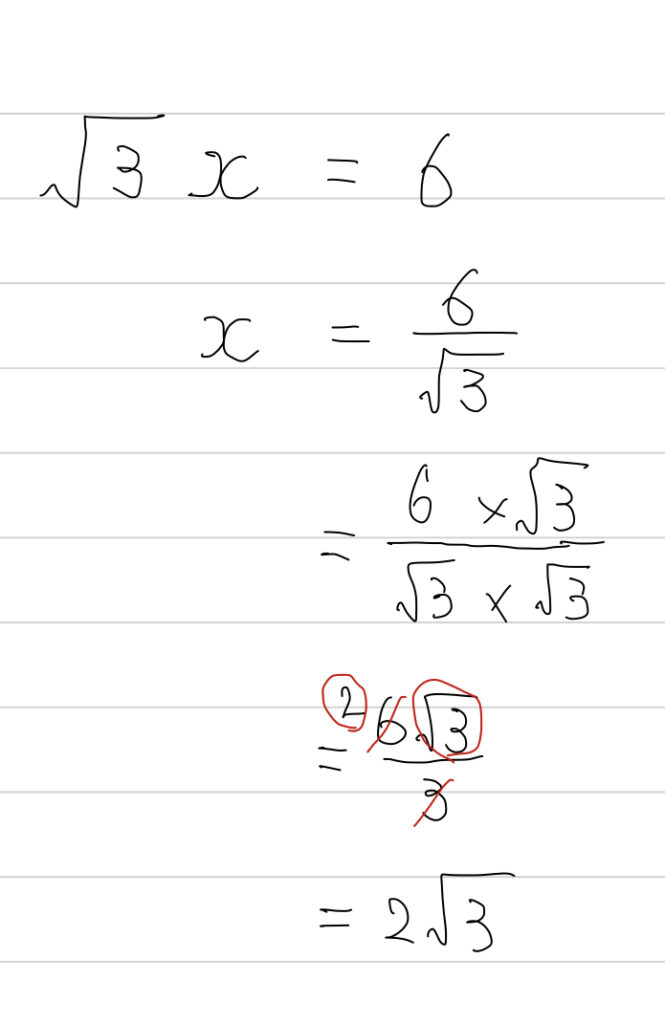
分母の有理化。「私はこの方法でやります」という人は、基本的な考え方が身についています。OKです。
しかしこの問題も、
「▲x=……」の形は、▲を整数にするとラク
という工夫をすると……
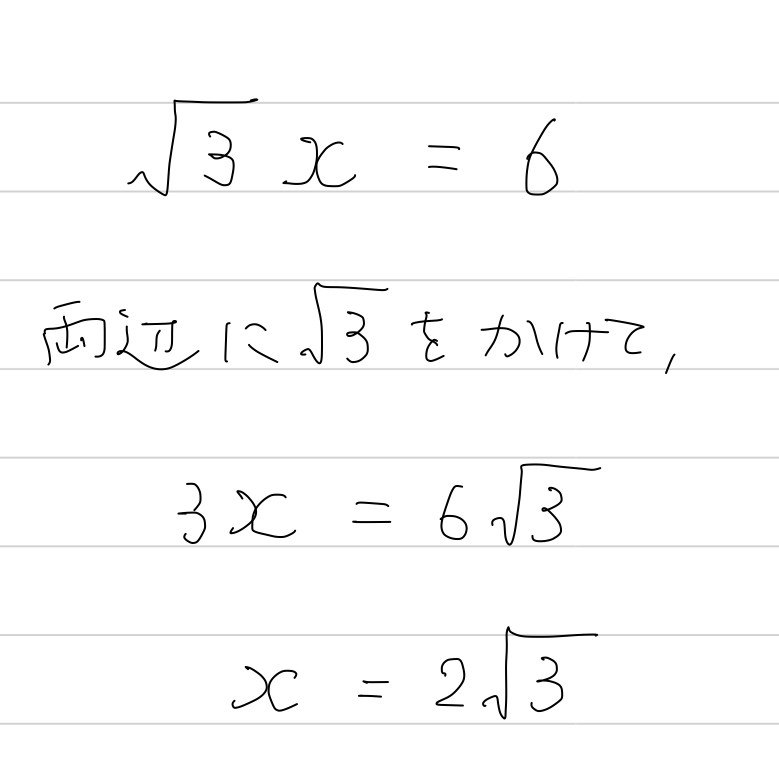
なんと分母の有理化をしなくて済むんです、分数が出てこないから。
分母の有理化はミスが出やすいからね、できれば避けたい人もいるでしょう。
2つの解き方を並べてみます。
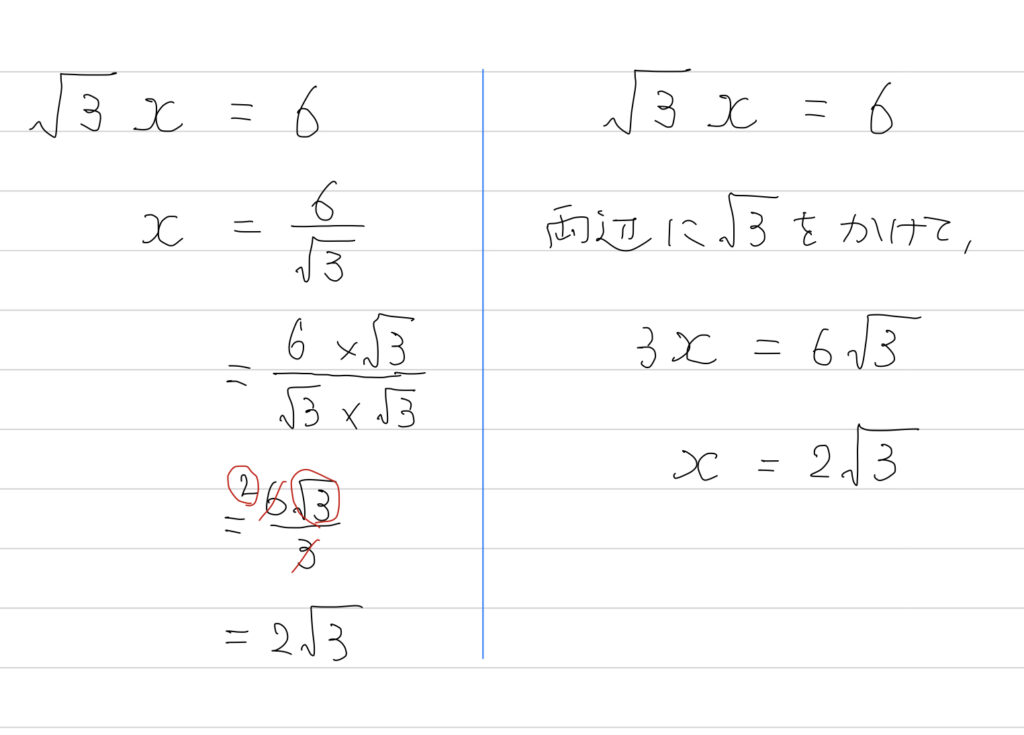
入試本番で、見直しをしていると想像して。左右どっちが見直ししやすい?
もうちょっと難しい例題を。三平方の定理の難しめの問題に挑戦していると、こういう式が出てくるよね。
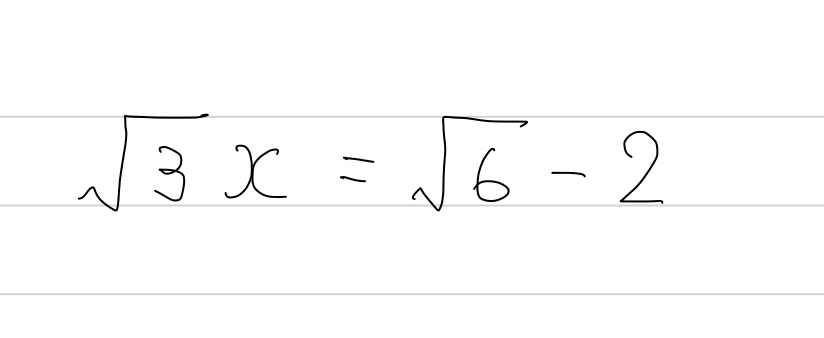
この方程式さえ解ければゴール……なんだけど、これがなかなか厄介なんですよね。できれば時間をかけてじっくりミスしないようにやりたいところ。
しかし、入試本番では、これを、
短時間で
確実に
さばかねばなりません。
まずは、分母の有理化をする方法。
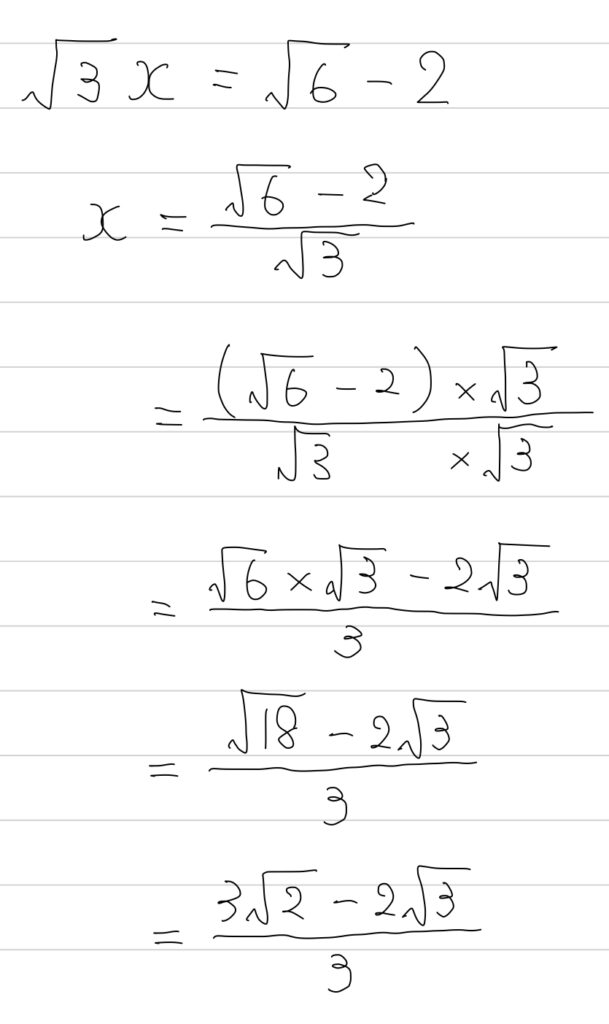
間違ってはいないんだけど、見ていてヒヤヒヤします。どこか1つでも失敗したら、バツになっちゃいますからね。
次に、
「▲x=……」の形は、▲を整数にするとラク
という工夫をする方法。
両辺に √3 をかけてみましょう。

並べてみます。
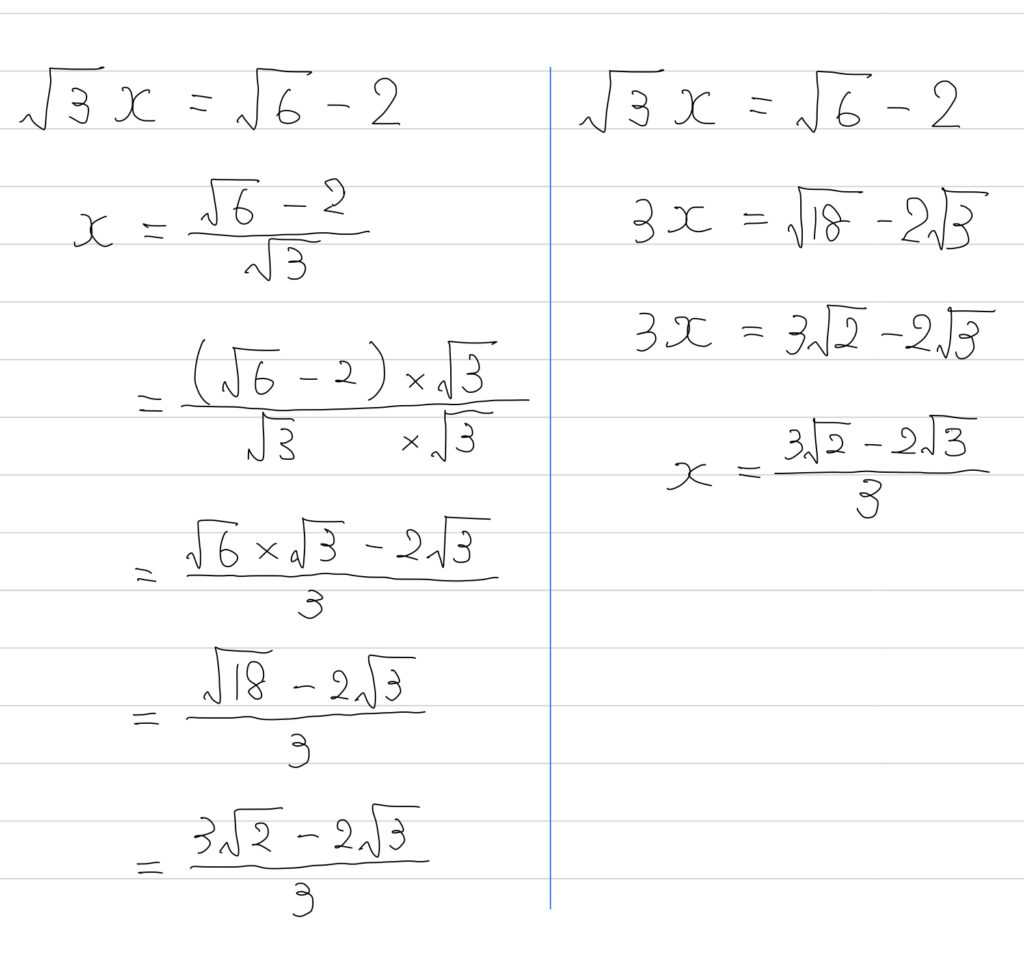
分母の有理化に自信がある人は、もちろんそれでOKです。正しい解を求められるなら何でもいいんですから。
「こんな方法もあるんだね」と、あなたのテクニックの1つに加えてみてね。
本日のまとめ。

以上、計算の工夫でした。
それでは今日はこのあたりで失礼します。どうぞ健やかな一日をお過ごしください。




この記事についてのコメント