なまはげおじさんです、こんにちは。
君津のさくら塾のブログへようこそ。
今日は数学のお話。中3生向けです。
これが正しい「仮定より」の使い方
3年さくらっ子、相似の証明にて。
ひとりひとりの答案をチェックしていたのですが、この春から入塾したさくらっ子が共通した間違いをしていることに気づきました。
それは、「仮定より」という言葉の使い方がわかっていないというもの。
例えば、
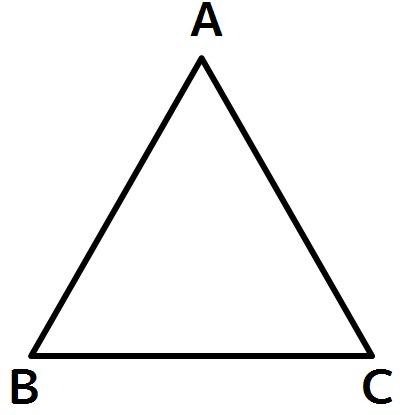
というような問題に対して、
仮定より、
∠B=∠C
とやってしまっているのです。
これはダメです、減点対象。
中3生のみなさん、どこがマズイかわかりますか?
証明は証拠だけじゃダメ
証明は、証拠(∠A=∠Bなど)を列挙するだけでは成立しません。
コナンくんの推理のように、なぜそう言い切れるのか、それを誰が読んでもわかるようにきちっと書く必要があります。
「合同な図形は対応する角の大きさが等しいので、」
「平行線の錯角は等しいので、」
「共通する辺なので、」
などなど、一つ一つの証拠について、その理由を書いていきます。
「仮定より、」
もその中のひとつ。
短くて使い勝手がいいので、つい深く考えずに書いてしまっている人もいるでしょう。
でもね、「仮定より、」って、書いていいのは2パターンしかないんですよ。知ってましたか?
仮定より
みんなが大好きな「仮定より、」は、いわば省略ですよ。「グダグダと長く説明しないけどわかるでしょ?」ってことですよ。
省略していいのは、次の2パターンだけ。
①問題文に書いてあること
(与えられた図にある)
②その図形の定義について
この2つだけなんです。
これら以外のときに「仮定より、」とやってしまうとバンバン減点されるというわけ。
もうちょっと具体的に。
①問題文に書いてあること
これはみなさんご存知ですな。
例えば、
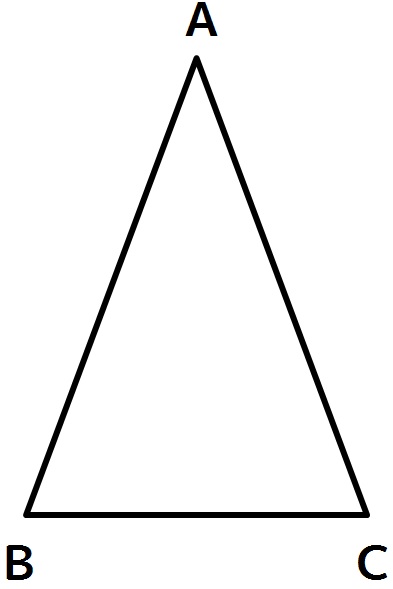
なんて問題があったとしたら、
仮定より、
AB=AC……①
と書いてOK。
だって書いてあるじゃん。
これはいいですよね。
案外知られていないのは次のパターン。
②その図形の定義について
図形の定義と「仮定より、」の関係がよくわかっていない人、多いです。
さっきの例で説明しましょうか。

3年生のみなさん、正三角形の定義って、何でしたか?
・
・
・
・
・
3つの辺の長さが等しい三角形、ですよね。
もしあなたが、AB=BCと書きたければ、
正三角形の3つの辺は等しいので、
AB=BC
などと書く必要はないのです。
短く、
仮定より、
AB=BC
とやってしまってOKということ。
混同している人がいそうなので指摘しておきますが、『正三角形の3つの角は等しい』というのは定義ではありません、それは性質です。
省略書きが許されるのは定義。
ですから、
仮定より、
∠B=∠C
なんて書いちゃダメなんです。
多少面倒でも、
正三角形の3つの角は等しいので、
∠B=∠C
ときっちり書く必要があるのです。
どうかな、スッキリしたかな。
試してみよう
ここまで読んでくれた中3生のあなたのために、練習用の問題を用意しましたよ。
2行だけで完成する、ごく基礎的な証明。
考えてみてね。

どうかな。
できたかな。
それでは、まずは良くない解答例。
証明)
仮定より、
∠B=∠C
このブログをちゃんと読んでくれた人なら、なぜこれが正解にならないか、わかりますよね。
では、OKな例。
証明)
二等辺三角形の2つの底角は等しいので、
∠B=∠C
はい、今日のお話はここまでです。
「仮定より、」の使い方、つかめたでしょうか。
せっかくなので、2年生のときに勉強したことの復習問題もおいておきますね。挑戦する人は、筆記用具を準備してください。

できれば2通りの証明を思いついてほしいですな。
解答例は下に。
解答例1。
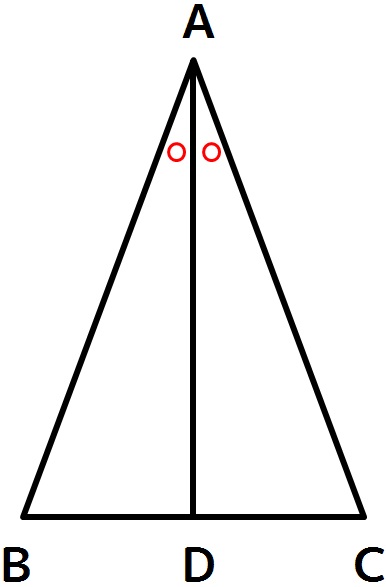
証明)
頂角Aの二等分線ADをひく。
△ABDと△ACDにおいて、
仮定より、
AB=AC…①
∠BAD=∠CAD…②
共通する辺なので、
AD=AD…③
①②③より、2組の辺とその間の角が、それぞれ等しいので、
△ABD≡△ACD
合同な図形の対応する角の大きさは等しいので、
∠ABD=∠ACD
解答例2。
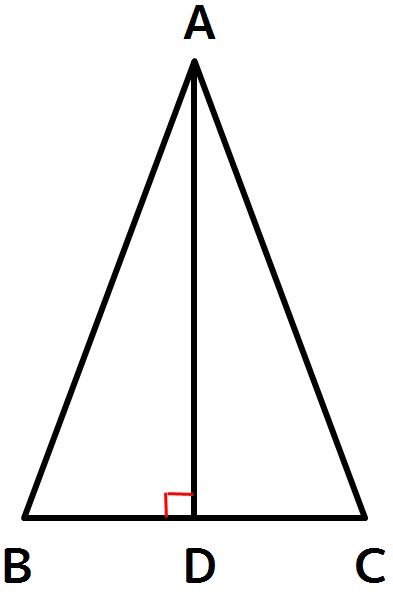
証明)
頂角からBCに垂線ADをひく。
△ABDと△ACDにおいて、
仮定より、
AB=AC…①
∠ADB=∠ADC=90°…②
共通する辺なので、
AD=AD…③
①②③より、直角三角形の斜辺と他の1辺が、それぞれ等しいので、
△ABD≡△ACD
合同な図形の対応する角の大きさは等しいので、
∠ABD=∠ACD
以上、証明についてのお話でした。
それでは今日はこのあたりで失礼します。どうぞ健やかな一日をお過ごしください。




この記事についてのコメント