不正車検はいけませんぞ。ローカルネタでごめんなさい、なまはげおじさんです、こんにちは。
さくら塾のブログへようこそ。
今日のお話は、中2・中3生向けのものです。教科書のコラムをとりあげています。保護者のみなさまは、今こういう勉強を中学校ではしているのか、という視点でご覧ください。
正方形の紙から正三角形ができる!?
このあたりの中学校で使われている数学の教科書は、啓林館という出版社のものです。その2年生バージョンである「未来へひろがる数学2」のP127には、このようなコラムが載っています。
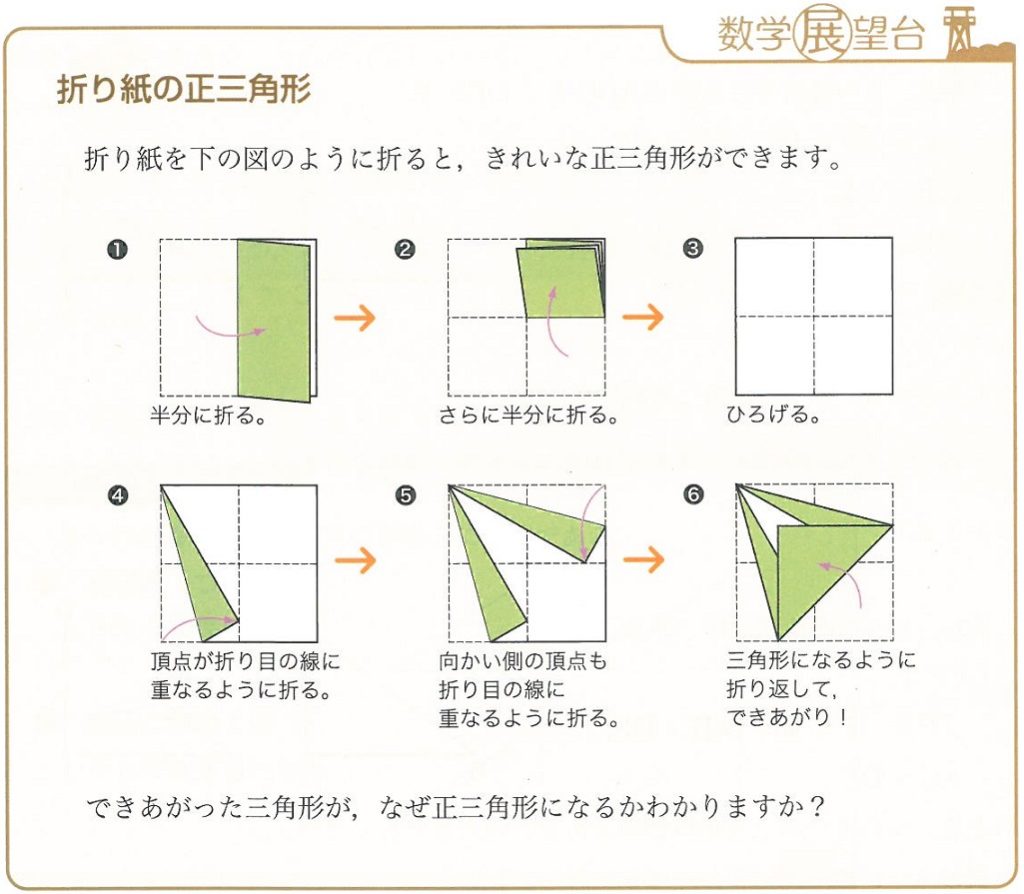
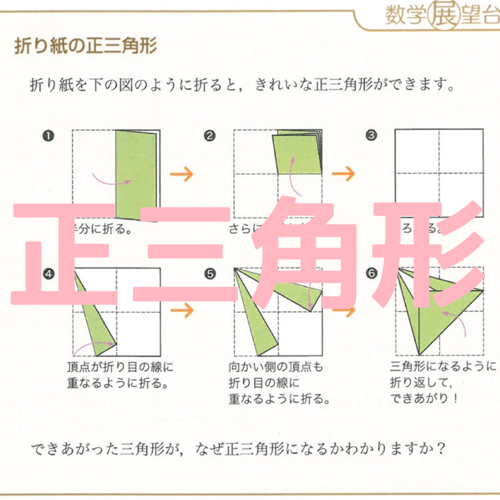
有名な折り紙ですね。ちびっ子でも知っているかもしれません。正方形の折り紙から、正三角形ができる。なんとも不思議なものです。実際にやらせてみて「ふしぎだ」「すごいな」と興味を持てるちびっ子なら、きっと中高でも数学が得意になるでしょうな。
さて、「できあがった三角形が、なぜ正三角形になるかわかりますか?」という問いかけを数学風に書き換えると、「できあがった三角形が正三角形であることを証明しなさい」となります。うむ、やってみましょう。
最初に言っときますね。これ、かなり面倒です。2年生・3年生のみなさん、気合いいれてついてきてくださいね。
証明の進め方
正三角形になることを証明するには、次の2つが考えられます。
ア 3つの辺がすべて等しいので、正三角形である
イ 3つの角がすべて等しいので、正三角形である
ア は正三角形の定義であり、イ は正三角形の性質です。ア・イ の2つを、正三角形になる条件、と考えてもOKです。この2つ以外にはルートは存在しません。
今回は、イ で攻めます。
おおまかな流れ
すべての角が等しいことを直接示すことができればカンタンなのですが、この問題ではそれはできません。最初に「かなり面倒」と書いた理由ですな。
そこで、2つのステップを踏もうと思います。
ステップ1
・二等辺三角形であることを示す
ステップ2
・その頂角が60度であることを示す
この2つのステップを踏むことができれば、
二等辺三角形の頂角が60度
↓
2つの底角もそれぞれ60度になる
↓
3つの角がすべて等しい
となり、「3つの角がすべて等しいので、正三角形である」とおしまいにすることができるわけです。
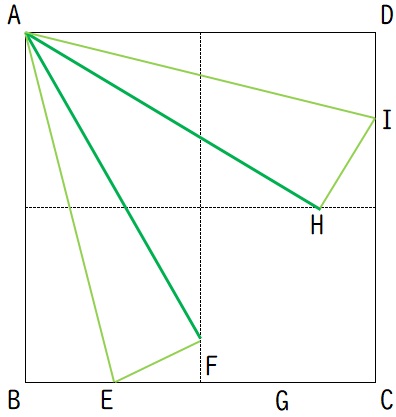
ここまでをまとめると、下図の△AEIについて、
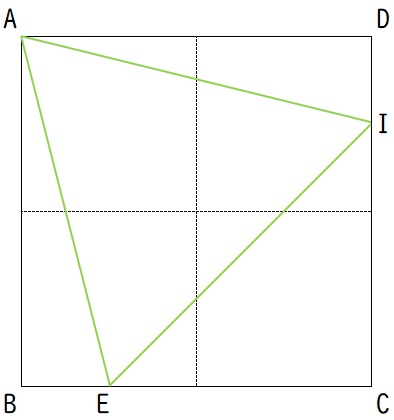
・AE=AIの二等辺三角形であること
・頂角EAI=60°であること
この2つのステップを踏んでいきます。それでは証明スタート!
証明しよう!
問題のコラムをもう一度貼っておきますね。

⑥の三角形が、正三角形であることを証明します。つまり、

上の図の△AEIが正三角形であることを証明するわけですね。いきますよー!
1.左右対称に下図のように折ってみる
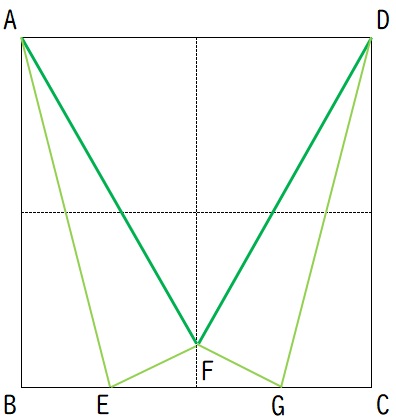
このとき、仮定より、
AB=AF……①
DC=DF……②
正方形はすべての辺が等しいので、
AB=DC=AD……③
①②③より、
AF=DF=AD
よって、△AFDは正三角形である。
正三角形の1つの内角は60°なので、
∠FAD=60°……④
2.∠BAE=∠FAE=15度であることを示す
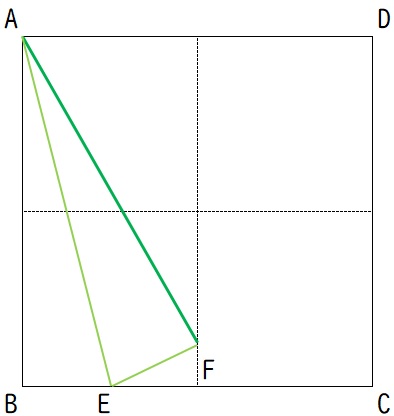
△ABEと△AFEにおいて、
仮定より、
AB=AF……⑤
∠ABE=∠AFE=90°……⑥
共通する辺なので、
AE=AE……⑦
①②③より、直角三角形の斜辺と他の1辺が、それぞれ等しいので、
△ABE≡△AFE
合同な図形は対応する角が等しいので、
∠BAE=∠BFE……⑧
④⑧より、
∠BAE=∠FAE=15°……⑨
3.△AEIが二等辺三角形であることを示す
同様に、
∠DAI=15°……⑩
△ABEと△ADIにおいて、
仮定より、
AB=AD……⑪
∠ABE=∠ADI=90°……⑫
⑨⑩⑪⑫より、1組の辺とその両端の角が、それぞれ等しいので、
△ABE≡△ADI
合同な図形は対応する辺が等しいので、
AE=AI
よって、△AEIは二等辺三角形である。
4.∠EAI=60度であることを示す

二等辺三角形AEIにおいて、
頂角AEIの大きさは、⑨⑩より、
∠EAI=60°
5.△EAIが正三角形であることを示す
よって、底角の大きさは、
(180°ー60°)÷2=60°
となり、3つの内角すべてが等しい。
したがって、△AEIは正三角形である。
おしまーい。長ーい。
おさらいすると、△AEIについて、
・AE=AI
・∠EAI=60°
この2つを説明できればOKとなるわけです。
以上、正方形の折り紙から正三角形ができることについての数学的な証明でした。ほかの証明の方法もあるかもしれません、考えてみてくださいね。
それでは今日はこのあたりで失礼します。どうぞ健やかな一日をお過ごしください。



この記事についてのコメント